MHB Find the altitude of the triangle with minimum area

[MarkFL]

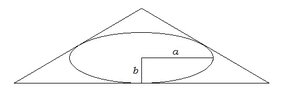
Consider the isosceles triangle circumscribed about the ellipse:

View attachment 1220

Find the altitude of the triangle when its area is minimized.

 

[Opalg]

[sp]Stretch the vertical axis by a factor $a/b$. Then the ellipse becomes a circle of radius $a$, and the area of the triangle is minimised when the triangle is equilateral with height $3a$. Now shrink the vertical axis back to where it started (by a factor $b/a$), and the minimising triangle then has height $3b.$[/sp]

 

[MarkFL]

[sp]Stretch the vertical axis by a factor $a/b$. Then the ellipse becomes a circle of radius $a$, and the area of the triangle is minimised when the triangle is equilateral with height $3a$. Now shrink the vertical axis back to where it started (by a factor $b/a$), and the minimising triangle then has height $3b.$[/sp]

Extremely clever, Chris, but then I would expect no less from you! (Sun)

Here is my solution:

Spoiler

I began by orienting the $xy$ axes at the center of the ellipse, and considered the right half of the triangle only. I then labeled the altitude of the resulting right triangle as $h$ and the length of its base as $B$.

The equation of the ellipse is then:

(1) $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

and the hypotenuse of the right triangle lies along the line:

(2) $$y=-\frac{h}{B}x+(h-b)$$

Substituting for $y$ from (2) into (1), we obtain the quadratic in $x$:

$$\left(\frac{a^2h^2}{B^2}+b^2 \right)x^2+\left(\frac{2a^2h(b-h)}{B} \right)x+a^2h(h-2b)=0$$

Since the ellipse is tangent to the hypotenuse, we require the discriminant to be zero, which implies:

$$h=\frac{2bB^2}{B^2-a^2}$$

And so the area $A$ of the right triangle may be written as as function of $B$ as follows:

$$A(B)=\frac{bB^3}{B^2-a^2}$$

Now, differentiating with respect to $B$ and equating the result to zero, we obtain:

$$A'(B)=\frac{bB^2\left(B^2-3a^2 \right)}{\left(B^2-a^2 \right)^2}=0$$

Since we must have $$a<B$$ we find:

$$B^2=3a^2$$

and hence:

$$h=\frac{2b\left(3a^2 \right)}{3a^2-a^2}=3b$$

It is easy to see this minimizes the area of the triangle by the first derivative test.