jamesbrewer
- 13
- 0
Homework Statement
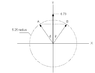
Two vectors A and B have the same magnitude of 5.25. If the sum of these two vectors gives a third vector equal to 6.73j, determine the angle between A and B.
Homework Equations
For some vector \vec{R}: |\vec{R}| = \sqrt{R_x^2 + R_y^2}
The Attempt at a Solution
I feel like I need to find the components of A and B, but I can't figure out how to do that with only the information given -- is it even possible?
I think the magnitude of the third vector is 6.73. Since there was no \hat{i} term given for \vec{R}, I would say that |\vec{R}| = \sqrt{R_x^2 + R_Y^2} = \sqrt{6.73^2} = 6.73.
Given the components of A and B, this would be easy to solve. Without them I am utterly lost. What am I missing?