Find moment arm of resultant force of two forces applied at two points

[zenterix]

Homework Statement

A force $\vec{F}_1=A\hat{j}$ is applied to $\vec{r}_1=a\hat{i}$ and a force $\vec{F}_2$ is applied to $\vec{r}_2=b\hat{j}$.

Find the arm $l$ of the resultant force relative to the origin.

Relevant Equations

The solution below coincides with the solution manual but at this point it is pretty clear that I arrived at this answer by chance (and incorrect methods).

We have

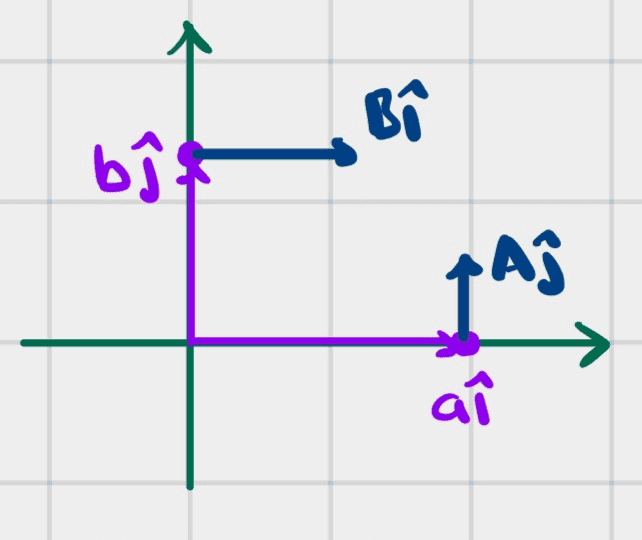
The torque about the origin is

$$\vec{\tau}=(aA-bB)\hat{k}\tag{1}$$

The resultant force is

$$\vec{F}_R=B\hat{i}+A\hat{j}\tag{2}$$

At this point, all I did was compute

$$|\vec{r}\times\vec{F}_R|=|\vec{r}||\vec{F}_R|\sin{\theta}=l|\vec{F}_R|=|\vec{\tau}|\tag{3}$$

which led to

$$l=\frac{|\vec{\tau}|}{|\vec{F}_R|}=\frac{\sqrt{(aA-bB)^2}}{\sqrt{A^2+B^2}}\tag{4}$$

which coincides with the solution manual

My question is about (3).

I wrote $|\vec{r}\times\vec{F}_R|=|\vec{\tau}|$ without thinking much about why I did that and now it seems pretty incorrect.

Here is my current thinking

1) We have a system of two particles of certain unknown masses $m_1$ and $m_2$.

2) The resultant force on the system works on the center of mass, which is at an unknown position $\vec{r}$ which appears in (3).

$$\vec{r}=\frac{m_1\vec{r}_1+m_2\vec{r}_2}{m_1+m_2}$$

$$\vec{r}\times\vec{F}_R=\frac{(m_1\vec{r}_1+m_2\vec{r}_2)\times (\vec{F}_1+\vec{F}_2)}{m_1+m_2}$$

$$=\frac{m_1\vec{\tau}_1+m_2\vec{\tau}_2+m_1\vec{r}_1\times\vec{F}_2+m_2\vec{r}_2\times \vec{F}_1}{m_1+m_2}$$

The two last terms in the numerator are zero in this problem.

Thus,

$$\vec{r}\times\vec{F}_R=\frac{m_1\vec{\tau}_1+m_2\vec{\tau}_2}{m_1+m_2}$$

$$|\vec{r}\times\vec{F}_R|=\frac{m_1aA-m_2bB}{m_1+m_2}=l|\vec{F}_R|$$

$$l=\frac{m_1aA-m_2bB}{(m_1+m_2)\sqrt{A^2+B^2}}$$

How did the solution manual arrive at the rhs of (4) as the solution? Ie, why are there no masses in their solution?

 

[haruspex]

At this point, all I did was compute

$$|\vec{r}\times\vec{F}_R|=|\vec{r}||\vec{F}_R|\sin{\theta}=l|\vec{F}_R|=|\vec{\tau}|\tag{3}$$

which led to

$$l=\frac{|\vec{\tau}|}{|\vec{F}_R|}=\frac{\sqrt{(aA-bB)^2}}{\sqrt{A^2+B^2}}\tag{4}$$

Looks fine to me.

How did the solution manual arrive at the rhs of (4) as the solution? Ie, why are there no masses in their solution?

What masses?

 

[zenterix]

What masses?

How can you have a force if there is no mass?

For translational motion calculations, the resultant force acts at the center of mass.

However, in light of another problem I posted about, it seems what I said in the OP about the resultant force being applied at the center of mass is not true when we are considering torques.

Thus, we can in fact equate the torque due to the resultant force and the sum of the torques due to the forces individually.

 

[haruspex]

How can you have a force if there is no mass?

In any real situation there will be masses, of course, but here we do not know any masses and we are not concerned with accelerations, so the masses are irrelevant.

For translational motion calculations, the resultant force acts at the center of mass.

Yes, for the purpose of calculating linear acceleration.
Any force with a given point of application can be treated as the sum of a force along a parallel line and a torque.
If $\vec F$ is applied at P and $PQ=\vec r$ then consider another force $\vec F'=\vec F$ applied at Q. The pair of forces $\vec F', -\vec F$ create a pure torque $\tau=\vec r\times\vec F$. Given any reference axis R, $\vec F$ has the same torque about R as does the combination of $\vec F'$ and the torque $-\tau$.
To find the acceleration of an object caused by $\vec F$, we can set Q to be its mass centre. A pure torque only rotates the body about its mass centre, so the acceleration of the mass centre is given by $\vec F=\vec F'=ma$.

Thus, we can in fact equate the torque due to the resultant force and the sum of the torques due to the forces individually.

Yes.