Find the angle for which both disks are no longer in contact

[Nicolas Gallardo]

Homework Statement

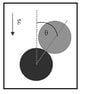
A mobile disk of radius R and mass M is moving above another immobile vertical disk of the same radius.
Initially the mobile disk is at rest at the highest point above the immobile disk and then it starts rolling without slipping. Assuming the mobile disk never slips, find the Θ for witch both disks are no longer in contact.

Homework Equations

V_cm=WR

The Attempt at a Solution

This is what I tried:

First the CoM of Disk 1(mobile disk)is at distance 2R from the origin(for me the origin is the CoM of Disk 2(immobile disk)
The Disk 1 is going to be at distance 2RcosΘ when they are no longer in contact.

In the other hand, we know both objects will no longer be in contact when N=0
After working with Newton's Secod Law :
i) mgsinΘ=0
j)N-mgcosΘ=ma_cp⇒ mgcosΘ=mv²/2R ⇒ (V_cm)²=2RgcosΘ

With this information I can apply conservation of energy:

Initially we have : mg2R
finally we are going to have: 1/2(Iw^2) + 1/2(m(v_cm)²)) + mg2RcosΘ

⇒ mg2R = 1/2(MR^2)(Vcm²)/R²) + 1/2(m2RgcosΘ) + mg2RcosΘ
⇒ mg2R = 1/2(MR^2)2RgcosΘ/R²) + 1/2(m2RgcosΘ) + mg2RcosΘ
⇒ 2= cosΘ + cosΘ + 2cosΘ

⇒ Θ=1/2... but the right answer is Θ= 4/7 what am I doing wrong?

 

[CWatters]

First the CoM of Disk 1(mobile disk)is at distance 2R from the origin(for me the origin is the CoM of Disk 2(immobile disk)
The Disk 1 is going to be at distance 2RcosΘ when they are no longer in contact.

I don't follow that.

I get they start with the COM separated by 2R. However as theta increases Cos(theta) becomes less than 1. So you are saying they somehow get closer together than 2R.

I haven't looked at the rest yet as it's gone midnight local time.

 

[Nicolas Gallardo]

I don't follow that.

I get they start with the COM separated by 2R. However as theta increases Cos(theta) becomes less than 1. So you are saying they somehow get closer together than 2R.

I haven't looked at the rest yet as it's gone midnight local time.

Yes initially the CoM are separated by 2R. But when they are about to separate the distance beween the origin(by origin I mean the reference to apply conservation of energy) and the CoM of Disk 1 is 2RcosΘ (trigonometry) may be I did my calculations wrong, but I did this just to apply conservation of energy, I needed to know the final position of the CoM of disk 1..

 

[Nathanael]

After working with Newton's Secod Law :
i) mgsenΘ=0

Assuming you meant sin not sen, its still nonsense to me, maybe you could explain where it comes from. (Although it clearly implies Θ = 0... which is not good.)

Other than that there’s only one mistake I see, you used I = mR^2 which applies for a ring not a disk.


(And technically the distance between the centers stays 2R until after contact is lost; just the vertical component shortens.)

 

[Nathanael]

You should be clear though that your “w” is V/R and not V/(2R) and justify why that is the correct rate. (The centripetal ω was V/(2R) so there’s two rates involved.)

 

[Nicolas Gallardo]

Assuming you meant sin not sen, its still nonsense to me, maybe you could explain where it comes from. (Although it clearly implies Θ = 0... which is not good.)

Other than that there’s only one mistake I see, you used I = mR^2 which applies for a ring not a disk.


(And technically the distance between the centers stays 2R until after contact is lost; just the vertical component shortens.)

You should be clear though that your “w” is V/R and not V/(2R) and justify why that is the correct rate. (The centripetal ω was V/(2R) so there’s two rates involved.)

That is the correct rate beacuse the CoM of disk 1 is at 2R from the CoM of disk 2, and disk1 is rotating with respect to the CoM of disk 2?

 

[Nicolas Gallardo]

Assuming you meant sin not sen, its still nonsense to me, maybe you could explain where it comes from. (Although it clearly implies Θ = 0... which is not good.)

Other than that there’s only one mistake I see, you used I = mR^2 which applies for a ring not a disk.


(And technically the distance between the centers stays 2R until after contact is lost; just the vertical component shortens.)

mgsen(theta)=0 is beacuse of how I used my coordinates system. There is no acceleration in the i-coordinate. I did it this way, so I only had to descompose the weight.

 

[Nathanael]

That is the correct rate beacuse the CoM of disk 1 is at 2R from the CoM of disk 2, and disk1 is rotating with respect to the CoM of disk 2?

You could say the CoM of disk 1 is rotating about disk 2, that’s how you get a_cp = V_cm²/(2R) which you used in “j)” (but didn’t share that step with us). This rotation rate is ω = V_cm/(2R)

But you can also say the disk is rotating about its center of mass at a rate w. This w is the one you want to use in the rotational part of the energy equation. You input w=2ω instead of w=ω. Did you do this on purpose? Why?

 

[Nicolas Gallardo]

You could say the CoM of disk 1 is rotating about disk 2, that’s how you get a_cp = V_cm²/(2R) which you used in “j)” (but didn’t share that step with us). This rotation rate is ω = V_cm/(2R)

But you can also say the disk is rotating about its center of mass at a rate w. This w is the one you want to use in the rotational part of the energy equation. You input w=2ω instead of w=ω. Did you do this on purpose? Why?

Firstly I would like to apologize for my lack of information given. In the other hand I did not input ''w=2ω'' anywhere, may be it was a typo mistake. I just used that the rotational energy on a solid is K_rot=(1/2)Iω².
Anyway thanks to you, I could find the answer. So I appreaciate your help. Sorry if it was a little confusing, english is not my native lengauge and I am doing my best for you to understand me.

 

[Nathanael]

I did not input ''w=2ω'' anywhere, may be it was a typo mistake. I just used that the rotational energy on a solid is K_rot=(1/2)Iω².

But if we have ω=V_cm/(2R) as above, then the correct answer should use K_rot = (1/2)I(2ω)² because the disk rotates about its center at twice the rate that its center rotates about the other center.
It’s part of the problem to realize that, but I guess you just coincidentally left out the 1/2 factor.

Sometimes we get the right answer the wrong way. It’s important to make each step clear.