Find the Angle Theta for E Field in Glass Below Boundary | E Field Problem

[austinmw89]

Problem statement:
The E field measured just above a glass plate is equal to 2 V/m in magnitude and is direct at 45° away from the boundary, as shown in the figure. The magnitude of the E field measured just below the boundary is equal to 3 V/m. Find the angle theta for the field in the glass just below the boundary.

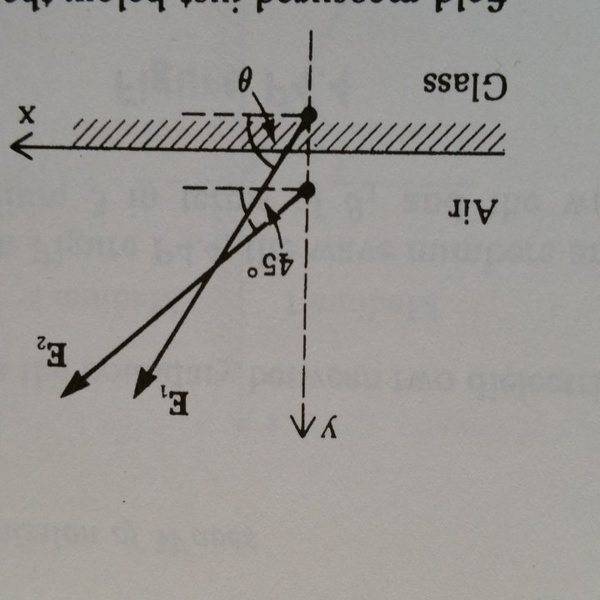
(sorry I don't know why uploading the image flipped it upside down)

I have the solution from the manual for this problem, but I still don't understand it. I'd really appreciate if someone could explain the beginning set-up of the solution:

E_1tan = E_2tan -> E_1cos(theta)=E_2cos(45°) -> cos(theta) = (E_2/E_1)*(sqrt(2)/2) -> theta = 61.9°.

I can follow the math from the second step, but my geometry is pretty rusty and I don't understand how they start with the tangents and also how they go from tangents to cosines.

 

[blue_leaf77]

"tan" stands for tangential, the tangential component of the E field to the boundary. You simply have to use the EM field boundary conditions. You basically have two options of which boundary conditions (there are 4 of them) will be helpful for this problem. Since you are given the E fields, the relevant boundary conditions are those involving the components of E field:
$$(i) \hspace{2mm} \epsilon_1 E_1^{\perp} - \epsilon_2 E_2^{\perp} = \sigma_f$$
$$ (ii) \hspace{2mm} \mathbf{E_1}^{\parallel} = \mathbf{E_2}^{\parallel}$$
Now since you are not given the permittivities $\epsilon$ and also the free charge distribution $\sigma_f$ , the best candidate to choose is the second one.

 

[austinmw89]

So if the boundary condition for the E field is [normal X (E_1 - E_2) = 0] I get [normal X E_1 = normal X E_2]. How do I go from this to tangent?

 

[blue_leaf77]

The normal and tangential boundary conditions are independent of each other, see my edited previous comment to see why the conditions for the normal components should not be used in this case.

 

[deskswirl]

The tangential components of the electric field must be continuous across any interface. So the component of the electric field inside the glass tangential to the interface E_1 Cos(\theta) must be equal to the tangential component of the electric field in air E_2 Cos(\Pi/4). Equating the two and solving for the angle \theta gives your result.

Reason: In order for the field (electric or magnetic) to be completely specified in both glass and air (or any material for that matter) the tangential field components must be continuous across any interface. This is know as the Uniqueness Theorem.

 

[austinmw89]

Thank you both