Find the area of the quadrilateral PQRS

[anemone]

The convex quadrilateral $ABCD$ has area 1, and $AB$ is produced to $P$, $BC$ to $Q$, $CD$ to $R$, and $DA$ to $S$, such that $AB=BP$, $BC=CQ$, $CD=DR$, and $DA=AS$. Find the area of the quadrilateral $PQRS$.

 

[Opalg]

[sp]Here is a solution using vectors. Choose the origin $O$ to be an interior point of $ABCD$ and let $a,b,c,d,p,q,r,s$ be the vectors representing the corresponding points. The area of the triangle $OAB$ is the magnitude of the cross product $a\times b$. The area of $ABCD$ is $|a\times b + b\times c + c\times d + d\times a|$. (Note that the four cross product vectors are all oriented in the same direction – perpendicular to the plane of $ABCD$ – so their magnitudes add up.)

Next, $p = 2b-a$, $q = 2c-b$, $r = 2d-c$ and $s = 2a-d$. Thus the area of $PQRS$ is $$\bigl|(2b-a)\times(2c-b) + (2c-b)\times(2d-c) + (2d-c)\times(2a-d) + (2a-d)\times(2b-a)\bigr|.$$ Now use the facts that the cross product of a vector with itself is $0$ and that $b\times a = -a\times b$ to see that this expression reduces to $5|a\times b + b\times c + c\times d + d\times a|$. Therefore the area of $PQRS$ is $5$.[/sp]

 

[anemone]

[sp]Here is a solution using vectors. Choose the origin $O$ to be an interior point of $ABCD$ and let $a,b,c,d,p,q,r,s$ be the vectors representing the corresponding points. The area of the triangle $OAB$ is the magnitude of the cross product $a\times b$. The area of $ABCD$ is $|a\times b + b\times c + c\times d + d\times a|$. (Note that the four cross product vectors are all oriented in the same direction – perpendicular to the plane of $ABCD$ – so their magnitudes add up.)

Next, $p = 2b-a$, $q = 2c-b$, $r = 2d-c$ and $s = 2a-d$. Thus the area of $PQRS$ is $$\bigl|(2b-a)\times(2c-b) + (2c-b)\times(2d-c) + (2d-c)\times(2a-d) + (2a-d)\times(2b-a)\bigr|.$$ Now use the facts that the cross product of a vector with itself is $0$ and that $b\times a = -a\times b$ to see that this expression reduces to $5|a\times b + b\times c + c\times d + d\times a|$. Therefore the area of $PQRS$ is $5$.[/sp]

Awesome, Opalg!(Yes) And thanks for participating!:)

I still welcome others who want to solve it using other route!

 

[RLBrown]

This type of question implies that the answer is the same for all Convex Quads with Area=1.

Spoiler

Picking a convenient one -- square.

View attachment 3184

We see the answer is: The area of a square with side = square root of (1² + 2²).

 

[anemone]

This type of question implies that the answer is the same for all Convex Quads with Area=1.

Spoiler

Picking a convenient one -- square.

View attachment 3184

We see the answer is: The area of a square with side = square root of (1² + 2²).

Thanks for your diagram and your solution post, RLBrown.

Another solution that solved the problem using trigonometric method is shown below:

Spoiler

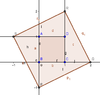
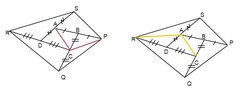
View attachment 3239
Consider the diagram on the left: [TABLE="class: grid, width: 800"]
[TR]
[TD]Note that the area of the triangles

$CBA=\dfrac{(CB)(AB)\sin \angle ABC}{2}$

and

$CBP=\dfrac{(CB)(BP)\sin \angle PBC}{2}$

are the same since $AB=BP$ and

$\begin{align*}\sin \angle PBC&=\sin (180^{\circ}-\angle ABC)\\&=\sin \angle ABC\end{align*}$.[/TD]
[TD]Also, the area of the triangles

$QCB=\dfrac{(QC)(CP)\sin \angle QCP}{2}$

and

$CBP=\dfrac{(CB)(CP)\sin \angle PBC}{2}$

are the same since $QC=CB$ and

$\begin{align*}\sin \angle PBC&=\sin (180^{\circ}-\angle QCP)\\&=\sin \angle QCP \end{align*}$.[/TD]
[TD]This tells us

$2\times \text{area of the triangle $ABC$}=\text{area of the triangle $QBP$}$.[/TD]
[/TR]
[/TABLE]

Similar argument could be applied to the diagram on the right so that:

[TABLE="class: grid"]
[TR]
[TD]Note that the area of the triangles

$RDA=\dfrac{(RD)(DA)\sin \angle RDA}{2}$

and

$CDA=\dfrac{(CD)(DA)\sin \angle CDA}{2}$

are the same since $RD=CD$ and

$\begin{align*}\sin \angle CDA&=\sin (180^{\circ}-\angle RDA)\\&=\sin \angle RDA\end{align*}$.[/TD]
[TD]Also, the area of the triangles

$RDA=\dfrac{(DA)(AR)\sin \angle DAR}{2}$

and

$RAS=\dfrac{(AR)(AS)\sin \angle RAS}{2}$

are the same since $DA=AS$ and

$\begin{align*}\sin \angle RAS&=\sin (180^{\circ}-\angle RDA)\\&=\sin \angle RDA \end{align*}$.[/TD]
[TD]This tells us

$2\times \text{area of the triangle $ADC$}=\text{area of the triangle $SRD$}$.[/TD]
[/TR]
[/TABLE]

Hence, we must have

$\begin{align*}\text{area of the quadrilateral $PQRS$}&=4(\text{area of the triangle $ADC$})+4(\text{area of the triangle $ADC$})+\text{area of the convex quadrilateral $ABCD$})\\&=4\text{area of the convex quadrilateral $ABCD$}+\text{area of the convex quadrilateral $ABCD$}\\&=5\end{align*}$