chwala
Gold Member
- 2,828
- 423
- Homework Statement
- See attached
- Relevant Equations
- sine rule
I was looking at this problem today, and i was trying to figure out its area with the given dimensions shown. First, is this even possible?...i later looked at the problem in detail and realized that i had missed out on some dimension that was given on the text.
Having said that, i would like to try and see if its possible to find the area of the quadrilateral with the given dimensions as indicated...i would nevertheless like to know whether this is possible. I will try look at it and share my working later...i will make use of sine, cosine rule and the angle property of parallelogram...
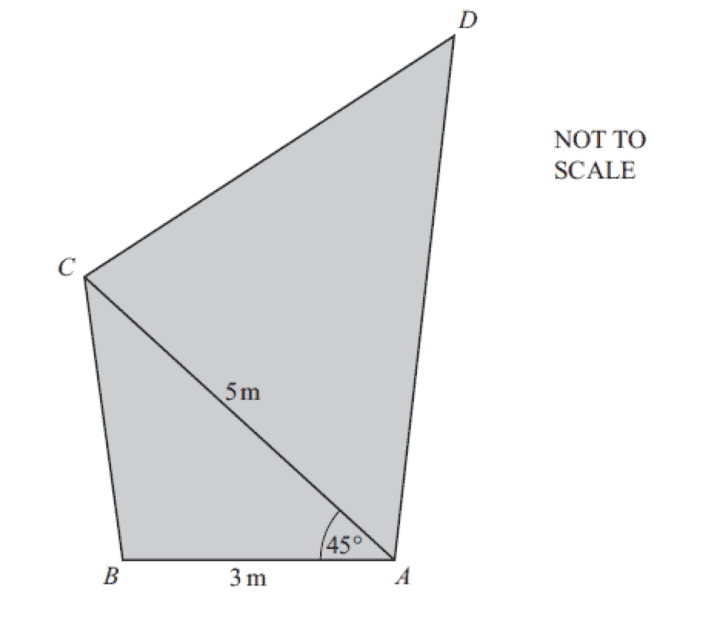
Having said that, i would like to try and see if its possible to find the area of the quadrilateral with the given dimensions as indicated...i would nevertheless like to know whether this is possible. I will try look at it and share my working later...i will make use of sine, cosine rule and the angle property of parallelogram...
Last edited: