Find the coefficient of restitution

[utkarshakash]

Homework Statement

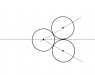
Two equal balls are in contact on a table. A third equal ball strikes them simultaneously and remains at rest after the impact. Show that the coefficient of restitution is 2/3.
I have attached an image for clarity of problem. Please open it.

Homework Equations

Conservation of Momentum

The Attempt at a Solution

Let the mass of balls be m and coefficient of restitution be e.

\frac{v_{2}}{vcosθ_{2}} = e

Also,
\frac{v_{1}}{vcosθ_{1}} = e

Applying Conservation of Momentum along X-axis

v=v_{1}cosθ_{1}+v_{2}cosθ_{2}
Along Y- axis
v_{1}sinθ_{1}=v_{2}sinθ_{2}

Substituting the value of v1 and v2 in the above equation
evcosθ_{1}sinθ_{1}=evcosθ_{2}sinθ_{2}
cosθ_{1}sinθ_{1}=cosθ_{2}sinθ_{2}

Multiplying 2 on both sides
sin2θ_{1}=sin2θ_{2}
Rearranging and simplifying
2cos(θ_{1}+θ_{2})sin(θ_{1}-θ_{2})=0
θ_{1}+θ_{2}=\frac{∏}{2}
θ_{1}-θ_{2}=0

θ_{1}=θ_{2} and θ_{1} = \frac{∏}{4}

Now substituting the value of θ1 in equation of momentum along X-axis

1=e(cos^{2}θ_{1}+cos^{2}θ_{2})
e=\frac{1}{cos^{2}θ_{1}+cos^{2}θ_{2}}
e=\frac{1}{2cos^{2}θ_{1}}
e=1

What's wrong here?

 

[klawlor419]

I will say first to reconsider your expressions for the coefficients of restitution. Also check the momentum conservation. Furthermore it may help to consider energy conservation as well. As this gives a further restraint on the values in the problem.

 

[utkarshakash]

I will say first to reconsider your expressions for the coefficients of restitution. Also check the momentum conservation. Furthermore it may help to consider energy conservation as well. As this gives a further restraint on the values in the problem.

energy conservation principle can't be applied here because the collision is not elastic. I also suspect something wrong in my expressions for coefficient of restitution. But I can't figure out what is it. Also I don't think that momentum conservation equations are wrong.

 

[klawlor419]

Well if it is indeed an inelastic collision than you are correct. It was not specified in your problem statement. You're off by a minus sign in one of your momentum conservation equations. The definition of the coefficient of restitution is fractional value of the ratio of speeds before and after a collision. You should be able to find the error by just considering this definition and looking at your expressions for, e.

 

[shutdo]

If the 3 balls are identical and the collisions occur simultaneously. You can immediately deduce that.
The lines of impacts of both collisions pass through the centres and therefore,
\theta_1=\theta_2=\frac{\pi}{6}\\<br /> and\\<br /> v_1=v_2
Then your answer is therefore e=\frac{2}{3}

 

[utkarshakash]

If the 3 balls are identical and the collisions occur simultaneously. You can immediately deduce that.
The lines of impacts of both collisions pass through the centres and therefore,
\theta_1=\theta_2=\frac{\pi}{6}\\<br /> and\\<br /> v_1=v_2
Then your answer is therefore e=\frac{2}{3}

Hey, why didn't I think it earlier! Thank You.