Find the coordinates of a point C from the given line, point and circle

[Mathman2013]

Homework Statement

Let the point P(2,8) be a point in xy-plane and line m: y = -0.75*x+3.25 be a line in the xy-plan. Using CAS, find The distance from a point P to a point B is 7 unites. Where the x coordinate of B is negative. Find the acute angle between PB and m. The distance PM, PC and PB form a triangle of area 20. The area of the formed triangle is 20. Find the coordinates of C.

Relevant Equations

y= mx+b and (x-a)^2+(y-b)^2=r^2

Let the point P(2,8) be a point in xy-plane and line m: y = -0.75*x+3.25 be a line in the xy-plan. The distance from a point P to a point B is 7 unites. Where the x coordinate of B is negative. Find the acute angle between PB and m.

To find B I then construct a circle of radius 7 with center C(2,8), and find that the coordinates of B to be (-4.92;6.94).

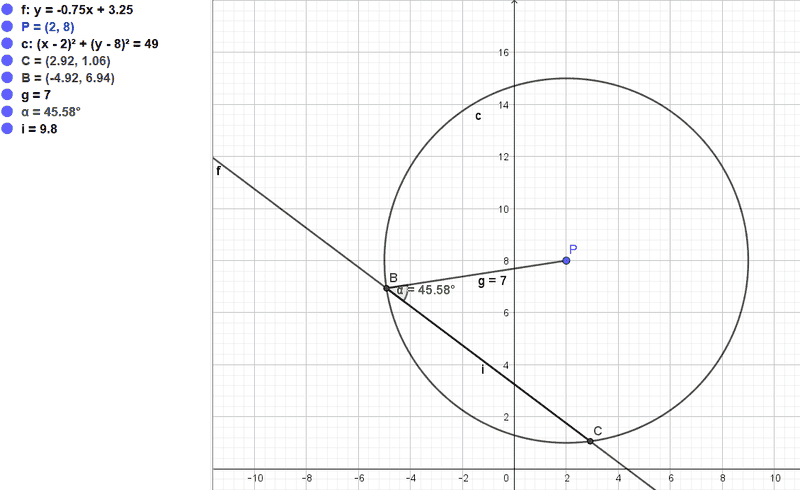
I use Geogebra, to find the acute angle to be 45.58 degrees.

My question if I need to find the coordinat C. Isn't the info that the area of the triangle is 20 redundant? Because I see from Geogebra that the coordinates for C must be (2.92; 1.06)

 

[phyzguy]

Why do you assume that C lies on the circle? I don't think it says that anywhere.

 

[Mathman2013]

Why do you assume that C lies on the circle? I don't think it says that anywhere.

Thank you for your answer. I look at the text again and the point C is suppose to be on line l too.

So my question how or can I use the information that the area of the triangle is suppose to be 20 to find C? Or is that information redundant?

 

[phyzguy]

So the point C is on the line, but not necessarily on the circle. So calculate the perpendicular distance from P to the line. This is the height of the triangle. Then the area of the triangle is Base*Height/2 = 20, so you can calculate the base, which is the distance BC. Since you know the coordinates of B, you should be able to find the point C.

 

[Mathman2013]

So the point C is on the line, but not necessarily on the circle. So calculate the perpendicular distance from P to the line. This is the height of the triangle. Then the area of the triangle is Base*Height/2 = 20, so you can calculate the base, which is the distance BC. Since you know the coordinates of B, you should be able to find the point C.

Just to understand your point. Since both B and C are on the l. Then the base of the triangle must be the distance from BC? If that that's the base. Then if I use the point-to-point distance formula, then I get a base of 9.8. And if the area of the triangle is 20 then the height is 9.8*height/2 = 20 then I get height = 4.08.

But the distance from P to the line l which should be the same as the height of the triangle 5? So what I am doing wrong?

 

[phyzguy]

I think you are still assuming that the point C is on the circle, but you don't know that.
I think you have correctly calculated the perpendicular distance from P to the line I as 5.0. This is the height. But you don't know the distance BC, since you don't know where the point C is. You have to find the point C so that the area of the triangle PBC is 20.

 

[Mathman2013]

I

I think you are still assuming that the point C is on the circle, but you don't know that.
I think you have correctly calculated the perpendicular distance from P to the line I as 5.0. This is the height. But you don't know the distance BC, since you don't know where the point C is. You have to find the point C so that the area of the triangle PBC is 20.

I think I got it now. if the height is 5 units = distance from line m to P. Then its is suppose to satisfy that (heigh*base)/2 = 20 meaning that (5*base)/2 = 20. Meaning that the base is suppose to be 8.

That must mean the distance from B to C is 8. Then I draw a circle with B as its center and radius 8, and find the intersection between this circle and m. which is the coordinate of C ?

 

[phyzguy]

Looks good to me !

 

[kuruman]

There is another way to do it using analytic geometry and without using the information that the area of the triangle is 20.

Any line perpendicular to line m has the equation $y=\dfrac{1}{0.75}x+q$. The one that goes through P(2,8) has intercept $q$ that is found from $$8=\frac{1}{0.75}2+q\implies q=\frac{16}{3}.$$Thus, the perpendicular line h in post #7 has the equation $y=\dfrac{4}{3}x+\dfrac{16}{3}$.

We can now find the coordinates of the intersection E of lines m and h:
$$\frac{4}{3}x_E+\frac{16}{3}=-\frac{3}{4}x_E+\frac{13}{4}\implies x_E=-1\implies y_E=4.$$
The distance between points P and E is $d=\sqrt{ (2-(-1))^2+(8-4)^2}=\sqrt{9+16}=5.$
The angle of interest is given by $\alpha=\arcsin(5/7)=45.58^o$.