- #1
Natasha1
- 493
- 9
<Moderator's note: Member has been informed to separate different question into different threads in the future.>
1. Homework Statement
Please see picture attached...
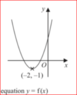
The diagram shows the curve with equation y = f (x)
The coordinates of the minimum point of the curve are (–2, –1)
(a) Write down the coordinates of the minimum point of the curve with equation
(i) y=f(x–5)
(ii) y = 0.5 f ( x )
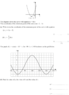
The graph of y=asin(x–b)+c (please see graph on picture)
b) Find the value of a, the value of b and the value of c.
(a) Write down the coordinates of the minimum point of the curve with equation
(i) y=f(x–5) Does the -5 move the graph 5 units to the right? Why is this? So the coordinates are (-7, -1)
(ii) y = 0.5 f(x) Does the times 0.5 widen the curve and has no impact on the minimum point so would stay (-2, 1)
b) Find the value of a, the value of b and the value of c.
Is a the magnitude? so a = 1
Is b the phase shift so -b shifts the graph by b units to the right so b = 360
Is c the vertical shift which is c = -1
Please explain :). Thank you in advance...
1. Homework Statement
Please see picture attached...
The diagram shows the curve with equation y = f (x)
The coordinates of the minimum point of the curve are (–2, –1)
(a) Write down the coordinates of the minimum point of the curve with equation
(i) y=f(x–5)
(ii) y = 0.5 f ( x )
The graph of y=asin(x–b)+c (please see graph on picture)
b) Find the value of a, the value of b and the value of c.
The Attempt at a Solution
(a) Write down the coordinates of the minimum point of the curve with equation
(i) y=f(x–5) Does the -5 move the graph 5 units to the right? Why is this? So the coordinates are (-7, -1)
(ii) y = 0.5 f(x) Does the times 0.5 widen the curve and has no impact on the minimum point so would stay (-2, 1)
b) Find the value of a, the value of b and the value of c.
Is a the magnitude? so a = 1
Is b the phase shift so -b shifts the graph by b units to the right so b = 360
Is c the vertical shift which is c = -1
Please explain :). Thank you in advance...
Attachments
Last edited by a moderator: