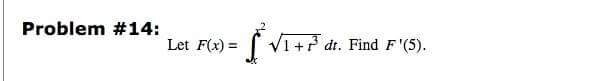MHB Find the derivative of the antiderivative

Click For Summary
To find the derivative of the antiderivative, the Fundamental Theorem of Calculus (FTOC) and the Chain Rule are essential. The discussion emphasizes the need to consider the bounds of the integral when applying these rules. The formula provided indicates that the derivative involves evaluating the function at the upper and lower bounds and multiplying by the derivatives of those bounds. Clarification is sought on whether this approach is correct for computing F'(x). A clear solution is requested to resolve the confusion surrounding the application of these concepts.
Umar
Messages
36
Reaction score
0
I know it seems pretty self explanatory, but I've tried to do this question and I've apparently gotten the wrong answer twice.

View attachment 6169

If anyone can give me a clear solution to the problem, that would be greatly aooreciated. I initially tried to follow a video I saw online, but I think there is something different I need to do considering the bounds. Maybe splitting the integral?
 

Attachments

  • received_1264397230298660.jpeg
    received_1264397230298660.jpeg
    3.3 KB · Views: 94
Physics news on Phys.org
By the FTOC and the Chain Rule, we have:

$$\frac{d}{dx}\int_{g(x)}^{h(x)} f(t)\,dt=f(h(x))\frac{dh}{dx}-f(g(x))\frac{dg}{dx}$$

Can you use this rule to compute $F'(x)$?
 

Similar threads

I Difference between integral and antiderivative?
  • · Replies 6 ·
Replies
6
Views
5K
I Why is the integral of ##\arcsin(\sin(x))## so divisive?
  • · Replies 3 ·
Replies
3
Views
2K
A The ``kinematic equation'' of fluid flows
  • · Replies 13 ·
Replies
13
Views
2K
MHB Find the Derivative of a Function: Step-by-Step Guide for Beginners
  • · Replies 15 ·
Replies
15
Views
3K
MHB Find the derivative using implicit differentiation (with inverse trig functions)
  • · Replies 2 ·
Replies
2
Views
2K
B Having trouble deriving the volume of an elliptical ring toroid
  • · Replies 4 ·
Replies
4
Views
3K
I Where Did I Go Wrong in Deriving Pi Using Calculus?
  • · Replies 6 ·
Replies
6
Views
4K
How can I do integrals by just eyeing them?
  • · Replies 5 ·
Replies
5
Views
2K
B Area under a sine integral graph
  • · Replies 8 ·
Replies
8
Views
2K
How much rigor upon first exposure?
  • · Replies 15 ·
Replies
15
Views
3K