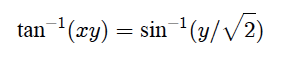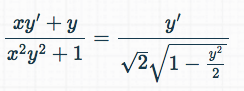Find the derivative using implicit differentiation (with inverse trig functions)

[Umar]

Here is the question:

View attachment 6100

This is the step I came to after taking the derivatives and doing some simplification:

View attachment 6101

^ I did the work myself on paper, I just couldn't type out the whole thing clearly so that anyone else can see what I'm referring too... so I used some online tool to show that step.

Now, my main concern here is solving for y', or essentially, dy/dx. I have tried numerous ways, but the math gets too ugly.
If anyone could please give this a try as soon as possible, that would be extremely appreciated!

 

[Euge]

Hi Umar,

The denominator of the right hand side of your equation is $\sqrt{2-y^2}$ by the rule $\sqrt{a}\sqrt{b} = \sqrt{ab}$. The left hand side can be written

$$\frac{y}{x^2y^2 + 1} + \left(\frac{x}{x^2y^2 + 1}\right)y'$$

So you have a linear equation in the form $A + By' = Cy'$ where

$$A = \frac{y}{x^2y^2 + 1},\quad B = \frac{x}{x^2y^2 + 1},\quad \text{and}\quad C = \frac{1}{\sqrt{2-y^2}}$$

We have $A = Cy' - By'$, or $A = (C - B)y'$. Show that $$C - B = \frac{x^2y^2 + 1 - x\sqrt{2-y^2}}{(x^2y^2 + 1)\sqrt{2-y^2}}$$ and complete the steps to obtain

$$y' = \frac{y\sqrt{2-y^2}}{x^2y^2 + 1 - x\sqrt{2-y^2}}$$

 

[Umar]

Hi Umar,

The denominator of the right hand side of your equation is $\sqrt{2-y^2}$ by the rule $\sqrt{a}\sqrt{b} = \sqrt{ab}$. The left hand side can be written

$$\frac{y}{x^2y^2 + 1} + \left(\frac{x}{x^2y^2 + 1}\right)y'$$

So you have a linear equation in the form $A + By' = Cy'$ where

$$A = \frac{y}{x^2y^2 + 1},\quad B = \frac{x}{x^2y^2 + 1},\quad \text{and}\quad C = \frac{1}{\sqrt{2-y^2}}$$

We have $A = Cy' - By'$, or $A = (C - B)y'$. Show that $$C - B = \frac{x^2y^2 + 1 - x\sqrt{2-y^2}}{(x^2y^2 + 1)\sqrt{2-y^2}}$$ and complete the steps to obtain

$$y' = \frac{y\sqrt{2-y^2}}{x^2y^2 + 1 - x\sqrt{2-y^2}}$$

Wow! Thank you so much. You explained it with so much simplicity that it never really looked hard at all. Thank you!