Find the differential equation

[MatinSAR]

Homework Statement

Find the differential equation of a family of straight lines that are tangent to the circle x^2+y^2=c^2?

Relevant Equations

Circle equation , mm'=-1,y-y1=m(x-x1)

Hi ... I have written the equation of family of straight lines which are tangent to the circle as :
y=(-m/n)x+(m^2/n)+n
line intersects circle at : (m,n)

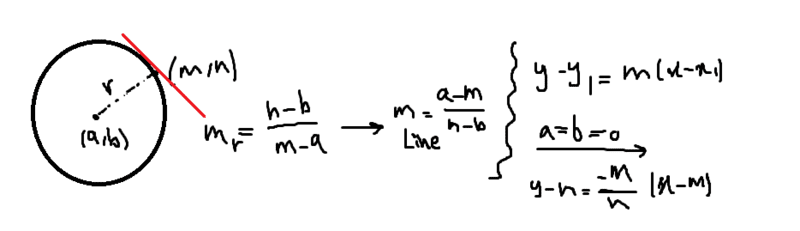
But I can't understand how to find differential equation of this ...

I will be appreciated if anyone has extra time to give me a little guidance on this question.

 

[Office_Shredder]

I think the generic goal here is to rewrite the equation as lhs is a function of the coordinates, and rhs is a function of only the parameter that you pick to set which curve you have, and then you differentiate. Then integrating both sides gives you lhs = arbitrary number, and the choice of number sets your parameter (by inverting the function on the rhs)

You have two parameters (m and n) so you're in trouble to start. Your real parameter that picks your curve is the angle on the circle.

Does your differential equation have to be in Cartesian coordinates? I think it's a lot more natural in polar coordinates since you're trying to isolate an angle.

Step one is to write down the equation of a line in polar coordinates
Remember the tangent line to the circle is the set of points which in vector form are radius vector + something perpendicular to the radius vector. This means it's the set of points which, when you take the dot product with the radius vector of your set angle, gives you $c^2$.

This actually gives you a really nice and simple representation of an arbitrary line perpendicular to the circle at angle $\alpha$ (remember the dot product can be computed using the lengths of the vectors and the angle between them!) I'll stop here and give you a chance to figure out the equation and solve the problem from here, let me know

 

[Delta2]

I am not sure what the problem is asking for, the differential equation of any family of straight lines is $$\frac{dy}{dx}=c$$ where c an arbitrary constant. Unless the problems wants to identify c in terms of the coordinates x and y of a point of circle. Yes it is $$c=-\frac{x}{y}$$ where (x,y) a point on the circle (or $-\frac{m}{n}$ since you used (m,n) for the point on circle.

 

[Delta2]

BTW, what you did to find the general equation of tangent line is not wrong, but you could do it another way: Find the derivative $\frac{dy}{dx}$ of the equation of the circle (by implicit differentiation of the equation of the circle), then the equation of the tangent line that passes at point (x,y) of the circle is $$Y-y=\frac{dy}{dx}(X-x)$$.

I used capital X and Y for a point of the tangent line and small x and y for a point of the circle.

 

[MatinSAR]

Step one is to write down the equation of a line in polar coordinates

Thank you ... But can you share a link which describes how to write the equation of a line in polar coordinates?

I used capital X and Y for a point of the tangent line and small x and y for a point of the circle.

Thank you.

 

[Delta2]

@Office_Shredder the differential equation you proposing, will have differentiation with respect to which variable? If I understand well you mean differentiation with respect to some angle but what angle i didnt quite understand.

 

[Office_Shredder]

@Office_Shredder the differential equation you proposing, will have differentiation with respect to which variable? If I understand well you mean differentiation with respect to some angle but what angle i didnt quite understand.

You should be able to describe an arbitrary line at $f(r,\theta)= C$ for some constant $C$ that only depends on your initial parameter (th angle that your point on the circle was at ). Then you can use implicit differentiation, just take the derivative with respect to either r or $\theta$ to be honest (though I think $\theta$ is more natural).

If you really need this to be in x and y terms you can turn $r$ and $\theta$ back into $x$ and $y$ and then differentiate with respect to $x$.

 

[Office_Shredder]

Thank you ... But can you share a link which describes how to write the equation of a line in polar coordinates?

Thank you.

Do you know what I mean when I say 'the set of points on the tangent line are the set of points for which the dot product with $(m,n)$ is $c^2$?

If so I can hit you with a linear algebra derivation, if not I'll have to think about the right way to present it.

Edit: an elementary construction. Suppose in polar coordinates the point on the circle is at $(c,\alpha)$ - $c$ is the distance from the origin and $\alpha$ is the angle from the x axis. Now pick a random angle $\theta$ and consider the choice of $r$ such that $(r,\theta)$ is on the line. You now have a right triangle - the radius line segment between the origin and $(c,\alpha)$, the line segment between the origin and $(r,\theta)$ and the line segment on the tangent line between $(c,\alpha)$ and $(r,\theta)$. Write down a trigonometric equation that this triangle satisfies. (What is the angle at the origin?)