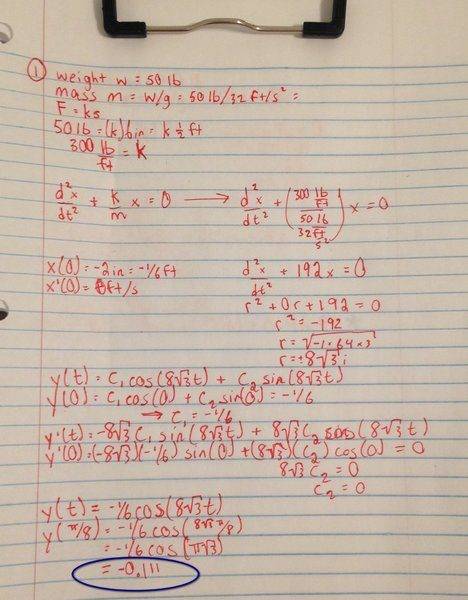Find the displacement from equilibrium after some time

[Mason Smith]

Homework Statement

A 50 lb weight is attached to the end of a spring. The spring is stretched 6 inches. Find the displacement from equilibrium of the weight after (π/8) seconds, if the weight is released from a point 2 inches above the equilibrium position. Round to the nearest length of a foot.
​

Homework Equations

(d²/dt²) + (k/m)x =0
mass m = w/g, where g = 32 ft/s²
F=ks, where k is the spring constant and s is how much the spring is stretched​

The Attempt at a Solution

My professor says that the answer is 0.2 ft. However, I am getting 0.11 ft.

 

[Orodruin]

In the future, please type out your attempt instead of just attaching an image of your work. (See the homework guidelines, item 5.)

What happened here?

In general, you should try not to insert numbers in the beginning of your solution - it makes it easy for errors to propagate without any easy means of checking your computations other than checking every single step. Give names to your knowns and unknowns and keep them until you have an expression for your sought quantity in terms of known quantities. Then, and only then, should you start inserting numerical values.

 

[Chandra Prayaga]

Isn't something wrong in your calculation of the spring cpnstant?