Nemo1
- 62
- 0
Hi Community,
I have this question.
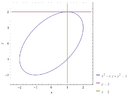
View attachment 5059I start by creating the derivative,
$$\d{}{x}(x^2-xy+y^2) = \d{}{x}(3) $$
and solve for $$\d{}{x}(3) $$ = 0 (Derivative of a constant is alway 0)
I understand how to solve the derivative of
$$\d{}{x}(x^2-xy+y^2)$$
and get $$2x-y$$
In the worked example it says:
$$2x-y-x\d{}{x}+2y\d{}{x}=0 \implies 2x-y=(x-2y)\d{y}{x}$$
Which becomes,
$$\d{y}{x}=\frac{2x-y}{x-2y}$$
I am lost at the previous step as I don't know where $$-x\d{y}{x}$$ and the $$+2y\d{y}{x}$$ come from?
I am wondering if I should be using the sum/differential rule $$(f \pm g)^{\prime}= f^{\prime} \pm g^{\prime}$$
I would like to fully understand the process for finding the derivative and how to plug it into solve for the tangent and normal to lines.
Many thanks for your time in advance.
Nemo
I have this question.
View attachment 5059I start by creating the derivative,
$$\d{}{x}(x^2-xy+y^2) = \d{}{x}(3) $$
and solve for $$\d{}{x}(3) $$ = 0 (Derivative of a constant is alway 0)
I understand how to solve the derivative of
$$\d{}{x}(x^2-xy+y^2)$$
and get $$2x-y$$
In the worked example it says:
$$2x-y-x\d{}{x}+2y\d{}{x}=0 \implies 2x-y=(x-2y)\d{y}{x}$$
Which becomes,
$$\d{y}{x}=\frac{2x-y}{x-2y}$$
I am lost at the previous step as I don't know where $$-x\d{y}{x}$$ and the $$+2y\d{y}{x}$$ come from?
I am wondering if I should be using the sum/differential rule $$(f \pm g)^{\prime}= f^{\prime} \pm g^{\prime}$$
I would like to fully understand the process for finding the derivative and how to plug it into solve for the tangent and normal to lines.
Many thanks for your time in advance.
Nemo