Find the escape velocity from 2 point charges

[r-swald]

Homework Statement

2 charges of -6nC are placed on the y-axis, on .005m above, and one .005m below the origin. A proton is launched from origin to the right along the x-axis. What is the escape velocity (m/s)?

Relevant Equations

PE = kQq / r
KE = mv^2 / 2

Below is the work I've attempted. I used 2 PE b'c there were 2 point charges, and only one KE b'c only the proton is moving. The final equation in case it's hard to see is V(esc) = sqrt (4kQq / mr).

I'm not sure if I did it right. Did I set up this equation right? and I am also not sure what to plug in for "r".

 

[TSny]

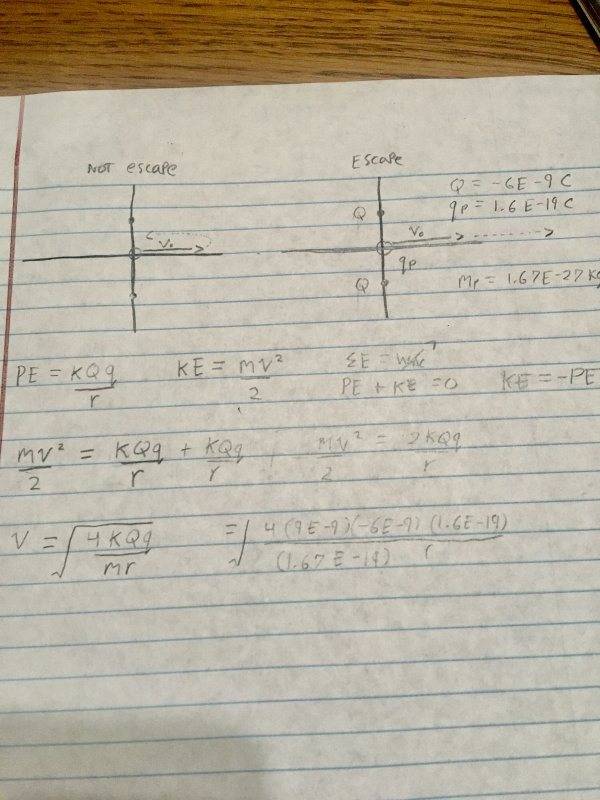
I'm not sure if I did it right. Did I set up this equation right? and I am also not sure what to plug in for "r".

You wrote that $\sum E = W_{\rm nc}$. But, this is not quite right.

$W_{\rm nc}$ is the work done by nonconservative forces as the system changes from some initial configuration to some final configuration. $W_{\rm nc}$ equals the change in total energy $E$ of the system as the system goes from the initial to final configuration.

That is, $\Delta E = W_{\rm nc}$ $\,\,\,\,\,$ (The $\Delta$ symbol is essential here.)

You know that $W_{\rm nc} = 0$ for this problem. Thus, $\Delta E =0$.

This means that $E_i = E_f$ $\,\,\,$ or $\,\,\,$ $KE_i+PE_i = KE_f + PE_f$ $\,\,\,\,$(conservation of energy)

You are given information about the initial configuration. You will need to decide what to take for the final configuration. Then consider what to write for $KE_i$, $PE_i$, $KE_f$, and $PE_f$.

If you are clear on the initial and final configurations, then you should be able to see what to use for $r$ in $PE_i$ and $PE_f$.

 

[r-swald]

You are given information about the initial configuration. You will need to decide what to take for the final configuration. Then consider what to write for $KE_i$, $PE_i$, $KE_f$, and $PE_f$.

If you are clear on the initial and final configurations, then you should be able to see what to use for $r$ in $PE_i$ and $PE_f$.

Ah, okay I mixed up change in and sum of.
I tried this again and I must be thinking screwy b'c the final KE I figured to be 0 since V final would be approaching 0, and the final PE I figured to be 0 since r final would approach infinity.
I also ended up with 0 initial PE b'c the top and bottom charges would cancel out.
I don't know what I'm doing.

 

[TSny]

Ah, okay I mixed up change in and sum of.
I tried this again and I must be thinking screwy b'c the final KE I figured to be 0 since V final would be approaching 0, and the final PE I figured to be 0 since r final would approach infinity.

That all sounds good.

I also ended up with 0 initial PE b'c the top and bottom charges would cancel out.

Think about this some more. What's the initial PE for the proton and the charge Q at y = .005 m? What 's the initial PE for the proton and the charge Q at y = -.005 m?

 

[r-swald]

That all sounds good.
Think about this some more. What's the initial PE for the proton and the charge Q at y = .005 m? What 's the initial PE for the proton and the charge Q at y = -.005 m?

Right, negative distance isn't possible, they'd only cancel if the charges were opposite. Thank you!