Find the intensity as function of y (interference between two propagating waves)

[LCSphysicist]

Homework Statement

.

Relevant Equations

.

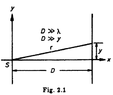
Let a spherical wave propagate from the origin, $y = ADcos(wt-2\pi r/ \lambda)/r$. Also, let a plane wave propagate parallel to the x axis, $y = Acos(wt-2\pi r/ \lambda)$. At x = D there is a flat screen perpendicular to the x axis. Find the interference at the point y on the screen as function of the interference at y=0.$$ E = (A e^{i(wt-2\pi D/ \lambda)} + AD/r e^{i(wt-2\pi r/ \lambda)} ) $$

$$ I = Q* (A^2 + (AD/r )^2 + 2AD*A/r cos{(2\pi D/ \lambda -2\pi r/ \lambda)} ) $$
Now, i pretend to use $$r \approx D$$ outside the cos, and $$r = \sqrt{ D^2 + y^2} \approx D(1+(y^2)/(2*D^2))$$ inside it.
So that $$ I = Q* (A^2 + A^2 + 2A^2 cos{(2\pi (y^2)/(2*D \lambda))} ) = 2A^2(1+cos{(2\pi (y^2)/(2*D \lambda))}) = 4A^2cos(\pi (y^2)/(2*D \lambda) = I_o cos(\pi (y^2)/(2D \lambda)) $$

THe problem is that the solutions is $I_o cos(\pi (y^2)/(D \lambda))$ And i have no idea where is my mistake.

 

[TSny]

$$2A^2(1+cos{(2\pi (y^2)/(2*D \lambda))}) = 4A^2cos(\pi (y^2)/(2*D \lambda) $$

Shouldn't the cosine function be squared on the right-hand side?

Otherwise, your work looks correct to me. In particular, I think the factor of 2 in the denominator of the argument of the cosine function is correct.

THe problem is that the solutions is $I_o cos(\pi (y^2)/(D \lambda))$ And i have no idea where is my mistake.

Did they have a square on the cosine function? If not, it is clearly wrong since the intensity cannot ever be negative.

 

[LCSphysicist]

Shouldn't the cosine function be squared on the right-hand side?

Otherwise, your work looks correct to me. In particular, I think the factor of 2 in the denominator of the argument of the cosine function is correct.

Did they have a square on the cosine function? If not, it is clearly wrong since the intensity cannot ever be negative.

Yes, i forgot the square in both answer. Thank you, so aparenttly the answer given by the book is wrong in fact.

 

[TSny]

Thank you, so aparenttly the answer given by the book is wrong in fact.

It appears that way to me. Maybe someone else will confirm it.