Richie Smash
- 293
- 15
Homework Statement
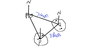
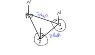
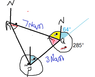
A ship sails 3 nautical miles from Port P on a course of 64° to Port Q, then changes course to 285° and sails a further 7 nautical miles to Port R.
(i) Draw a carefully labelled diagram of the entire route taken. Show the north direction where necessary.
(ii)Calculate the distance PR to three significant figures.
(iii) Determine the bearing of P from R.
Homework Equations
The Attempt at a Solution
I have drawn the diagram which i will post, as you can see I found angle PRQ to be 75° using alternate angles, and I found the exterior angles of the first two bearings by subtracting them from 360°.
But I can't seem to figure out the other two angles in the triangle to find the length, I could simply use the sine rule then°
PLEASE NOTE ON THE DIAGRAM THE ANGLE WHICH SAYS 375° SHOULD BE 285°
Attachments
Last edited: