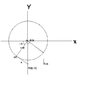
Find the length of this line associated with a circle

  • Context: Undergrad 
  • Thread starter Thread starter waqarrashid33
  • Start date Start date
  • Tags Tags
    Circle Length Line
Click For Summary
SUMMARY

The discussion focuses on calculating the length of a line segment (denoted as 'a') between points P1 and P2 associated with a circle, using the radius 'r' and angle 'A'. The key insight is that triangle 0P1P2 is a right-angled triangle, which allows for the application of trigonometric principles to derive the length of 'a'. Participants emphasize the importance of understanding the relationship between the radius, angle, and the properties of right triangles in circular geometry.

PREREQUISITES
  • Understanding of basic trigonometry, specifically sine and cosine functions.
  • Familiarity with properties of right-angled triangles.
  • Knowledge of circular geometry and the significance of radius and angles.
  • Ability to interpret geometric figures and diagrams.
NEXT STEPS
  • Study the sine and cosine rules in right-angled triangles.
  • Learn how to apply the Pythagorean theorem in circular contexts.
  • Explore the relationship between angles and arc lengths in circles.
  • Investigate the use of trigonometric functions in solving geometric problems.
USEFUL FOR

Students of geometry, mathematics educators, and anyone involved in solving problems related to circular shapes and trigonometric applications.

waqarrashid33
Messages
76
Reaction score
0
I am struck in a place where i have to find length of a line(a in fig i.e between P1 and P2) in the form of r and Angle A.
Refer to the figure:
All information available are r,O,P2,and A.
 

Attachments

  • research.JPG
    research.JPG
    9.5 KB · Views: 466
Physics news on Phys.org
hi waqarrashid33! :smile:

(try using the X2 button just above the Reply box :wink:)

hint: 0P1P2 is a right-angled triangle, and angle P10P2 = … ? :smile:
 

Similar threads

Undergrad Finding vertex of a 3D Triangle on a Plane
  • · Replies 3 ·
Replies
3
Views
2K
MHB Tangent line to circle making 30º with a second circle
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Simplify Condition for Chord Length Equals Angle?
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Geometry and algebraic equations
  • · Replies 4 ·
Replies
4
Views
2K
High School Can Curvature and Geodesics be Generalized in Higher Dimensions?
  • · Replies 10 ·
Replies
10
Views
3K
Undergrad Circumference of a circle on a spherical surface
  • · Replies 7 ·
Replies
7
Views
5K
High School Circle tangent to two lines and another circle
  • · Replies 2 ·
Replies
2
Views
4K
Undergrad Ave length of intersection of all lines through a unit cube
  • · Replies 4 ·
Replies
4
Views
3K
Graduate Interpreting photon correlations from independent sources
  • · Replies 178 ·
6
Replies
178
Views
9K
Pressure in branching pipes when diameters are not equal
  • · Replies 3 ·
Replies
3
Views
3K