- #1
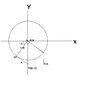
Find the length of this line associated with a circle
In summary, the formula for finding the length of a line associated with a circle is L = 2πr, where L is the length of the line and r is the radius of the circle. If you want to find the length of a line using the diameter of the circle, you can use the formula L = πd, where L is the length of the line and d is the diameter of the circle. The length of a line associated with a circle cannot be greater than the circumference of the circle and it cannot be negative. As the radius changes, the length of the line also changes proportionally, according to the formula L = 2πr.
- #2
tiny-tim
Science Advisor
Homework Helper
- 25,839
- 258
hi waqarrashid33! 
(try using the X2 button just above the Reply box)
hint: 0P1P2 is a right-angled triangle, and angle P10P2 = … ?
(try using the X2 button just above the Reply box
)hint: 0P1P2 is a right-angled triangle, and angle P10P2 = … ?
FAQ: Find the length of this line associated with a circle
What is the formula for finding the length of a line associated with a circle?
The formula for finding the length of a line associated with a circle is L = 2πr, where L is the length of the line and r is the radius of the circle.
How do you find the length of a line using the diameter of the circle?
To find the length of a line using the diameter of the circle, you can use the formula L = πd, where L is the length of the line and d is the diameter of the circle. This formula is derived from the fact that the diameter of a circle is twice the length of its radius.
Can the length of a line associated with a circle be greater than the circumference of the circle?
No, the length of the line associated with a circle cannot be greater than the circumference of the circle. The circumference of a circle is the distance around the outside of the circle, so any line associated with the circle must be a part of or equal to the circumference.
Can the length of a line associated with a circle be negative?
No, the length of a line associated with a circle cannot be negative. Length is a measure of distance and distance cannot be negative. If you encounter a negative value when finding the length of a line associated with a circle, it is likely due to a calculation error.
How does the length of a line associated with a circle change as the radius changes?
The length of a line associated with a circle is directly proportional to the radius. This means that as the radius increases, the length of the line also increases, and vice versa. This relationship is represented by the formula L = 2πr, where the length (L) is directly proportional to the radius (r).