Find the mass of the Sirius system

[Ithilrandir]

Homework Statement

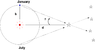
The trigonometric parallax of sirius (i.e, the angle subtended at sirius by the radius of the earth's orbit) is 0.378 degrees arc. Using this and data in Fig. 3-2, deduce as best you can the mass M of the sirius system in terms of that of the sun, and
a) assuming that the orbital plane is perpendicular to the line of sight, and
b) allowing for the actual tilt of the orbit.
Is your value in part (b) above an upper or lower limit (or either)?

Relevant Equations

...

I'll be focusing on mainly trying to find a way to solve part a, as I don't actually know how to account for the tilt.

When they said degrees arc I assume they're just saying degrees, so I found the distance of Earth to sirius to be around 1.50 x 10^8 km(radius of the earth), because of the small angle subtended.

I also found the period to be around 50+ years, by looking at the graph over the years. After that I'm stuck. In order to find the mass, I still need to know the radius of orbit of sirius, but I don't know how to read the graph to find that.

 

[haruspex]

I found the distance of Earth to sirius to be around 1.50 x 10^8 km(radius of the earth), because of the small angle subtended.

No, the small angle means it is much further away. Do you understand parallax?
Do you understand what a parsec is?

What is "5hus"?

 

[Ithilrandir]

No, the small angle means it is much further away. Do you understand parallax?
Do you understand what a parsec is?

What is "5hus"?

The 5hus was a typo which I've amended.

My notion of parallax is in this picture.

Are parsec related to the parallax?

 

[haruspex]

My notion of parallax is in this picture.

Ok, so if b is 1.5x10⁸km and the angle labelled π (terrible choice for a variable name) is 0.378 degrees then what is d?

Are parsec related to the parallax?

Yes. Look it up.

 

[Ithilrandir]

Ok, so if b is 1.5x10⁸km and the angle labelled π (terrible choice for a variable name) is 0.378 degrees then what is d?

Yes. Look it up.

d = b/tan 0.378.

I've looked up what parsec is. It's the distance from which 1AU subtends at one arc second.

 

[haruspex]

d = b/tan 0.3

Ok, so what is that in km?
By the way, for such small angles you don't need to bother with the tan function. Just write d = b/(angle in radians).

 

[Ithilrandir]

Ok, so what is that in km?
By the way, for such small angles you don't need to bother with the tan function. Just write d = b/(angle in radians).

3.97 x 10^8 km. How does this length relate to the graph in the question?

 

[Steve4Physics]

The trigonometric parallax of sirius (i.e, the angle subtended at sirius by the radius of the Earth's orbit) is 0.378 degrees arc.

No. The trigonometric parallax of Sirius is not 0.378 degrees of arc. It is 0.378 seconds of arc (often abbreviated to ‘arcsec’). That's a big difference.

Also, note that an expression such as ‘tan 0.378’ is meaningless unless you know what unit is being used for the angle. E.g.
tan(0.378 arcsec)
tan (0.378 radians)
tan (0.378º)
are completely different values.

By convention, if we leave out the unit we imply that the angle is in radians. So ‘tan 0.378’ would be interpreted as ‘tan(0.378 radians)’.

As a basic skill, you need to learn/understand how to change arc seconds to degrees and to radians. And you need to ensure that the value of an angle entered into a calculator is being entered in the appropriate unit.

As already noted by @haruspex, for small angles (as in this question), the tangent of the angle is, to a very good approximation, equal to the angle in radians.
E.g. tan(0.00123 rad) = 0.00123
So, for a small angle (value = A radians), it makes negligible difference whether you use tanA or A in calculations.

I am unfamiliar with your diagram in post #1 (Figure 3-2). There is no information about what is being plotted, the meaning of each axis or the meaning of the values around the edge of the ellipse.

[EDITs: Typo's fixed.]

 

[Ithilrandir]

I am unfamiliar with your diagram in post #1 (Figure 3-2). There is no information about what is being plotted, the meaning of each axis or the meaning of the values around the edge of the ellipse.

Thanks for the information in the first half.

The values around the edge are the point where the star is at at that year. As for the rest I don't know either, hence the post. This was all the information I have from the question.