- #1
uperkurk
- 167
- 0
Am I doing this correctly.
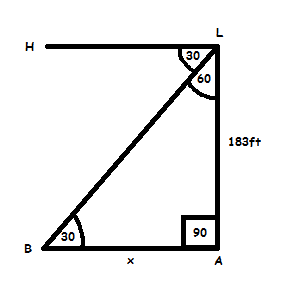
[tex]x \tan=\frac{183}{\tan 30}=317ft[/tex]
Also if it were the other way around and I needed to find the height but I already had the length would it just be
[tex]h \tan=\frac{x}{\tan 60}=hft[/tex]
[tex]x \tan=\frac{183}{\tan 30}=317ft[/tex]
Also if it were the other way around and I needed to find the height but I already had the length would it just be
[tex]h \tan=\frac{x}{\tan 60}=hft[/tex]