Find the particular solution of the second order differential equation

[chwala]

Homework Statement

see attached

Relevant Equations

understanding of homogenous and inhomegenous approach in solving ode's

My interest is on the highlighted (In Red). Otherwise the other steps are clear.

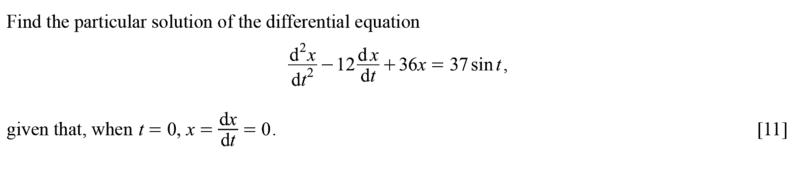
We have on that part of the problem,

$(-p\sin t -q\cos t)-12(p\cos t -q \sin t)+36p\sin t +36q\cos t = 37 \sin t + 0 \cos t$

Ah I just realized we are solving a simultaneous equation for $p$ and $q$ !

My problem was on how to get,

$-q-12p+36q =0$

Clear now.

Cheers if there is another approach to the problem. Laplace? I may need to refresh on it.

I now have (using laplace);

$s^2 \bar y -12(s\bar y -1) +36 \bar y = \dfrac {37}{s^2+1}$

$\bar y = \dfrac{37}{(s^2+1)(s-6)^2} - \dfrac{12}{(s-6)^2}$ will proceed later.

 

[Mark44]

Ah I just realized we are solving a simultaneous equation for p and q !

Hope you figured it out.
The idea is that a particular solution will be $x_p = A\sin(t) + B\cos(t)$
When you substitute the above into x'' - 12x' + 36x you'll have some combination of sine and cosine terms that must be identically equal to $37\sin(t)$. Since there is no cosine term, its coefficient must be zero. This will allow you to determine A and B.