Find the Radius of 4th Circle When All are Tangent: Hint d/2

[Andrei1]

View attachment 741
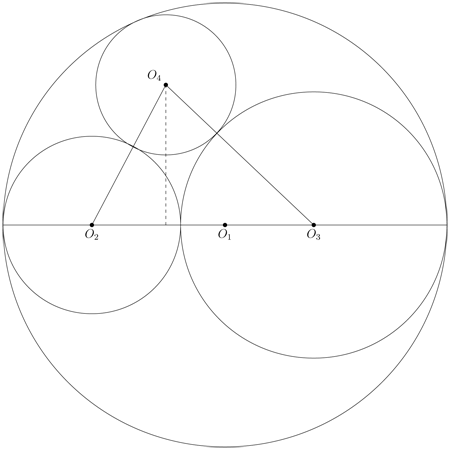
The centers of three circles are situated on a line. The center of the fourth circle is situated at given distance d from that line. What is the radius of the fourth circle if we know that each circle is tangent to other three. Please give me a hint, if you can. Answer: $$d/2.$$

 

[alyafey22]

Re: four circles

It is not clear what is d from the picture .

 

[mathmaniac1]

Re: four circles

It is not clear what is d from the picture .

The center of the fourth circle is situated at given distance d from that line.

I am also interested in the solution.

The center of the fourth circle is situated at given distance d from that line.

I am also interested in the solution.

Edit:

I also don't know where to start with this one.

But I really wonder why this works for all proportions in which the centre of the biggest circle is divided into.

It looks like d/2 is the radius of the 4th circle for all proportions (by my visualisation).

But to start working on it,I think I have to get to paper and pencil.

At first I would be looking for the case in which the centre of the big circle is divided into two equal parts as I assume it is easier to understand.

 

[Opalg]

The centers of three circles are situated on a line. The center of the fourth circle is situated at given distance d from that line. What is the radius of the fourth circle if we know that each circle is tangent to other three. Please give me a hint, if you can. Answer: $$d/2.$$

​

Write $r_1,\ r_2,\ r_3,\ r_4$ for the radii of the circles centred at $O_1,\ O_2,\ O_3,\ O_4$ respectively. Notice that $r_1 = r_2+r_3$. To calculate $r_4$ in terms of $r_2$ and $r_3$, use Descartes' theorem. For that, you need to use the curvatures $k_i = \pm1/r_i$ $(i=1,2,3,4)$. The first of these, $k_1$, will be negative (because the large circle touches the other three internally). Descartes' theorem says that $k_4 = k_1+k_2+k_3 \pm\sqrt{k_1k_2 + k_2k_3 + k_3k_1}$. When you substitute $k_1 = -1/(r_2+r_3)$, $k_i = 1/r_i$ for $i=2,3,4$, you find that the part inside the square root sign is zero (this corresponds to the fact that the centres $O_1,\ O_2,\ O_3$ are collinear). That gives you a formula for $r_4$ in terms of $r_2$ and $r_3$.

Now you have to bring in the distance $d$. I think the neatest way to do that is to use the fact that the area of triangle $O_2O_3O_4$ is $\frac12d(r_2+r_3)$. It is also given by Heron's formula in terms of $r_2,\ r_3,\ r_4$. Compare the two results and you will find that $r_4 = \frac12d$.