- #1
besi
- 2
- 2
New poster has been reminded to show their work on schoolwork problems
- Homework Statement
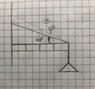
- Construction is in balance. The weight of the hanging body is 6 kg. The angle created between the wire and the wall is 30 degrees.
- Relevant Equations
- Find the thread tension in the construction shown in the figure.
I do not understand how this type of exercise is solved because I have not had a solution to such an example. I would ask you to show me the solution of this exercise step by step, so that I understand how to solve it. I appreciate your help. Thank you.
Last edited by a moderator: