SUMMARY
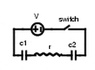
The time constant (Tau) of an RC circuit with two capacitors (C1 = 11 μF and C2 = 15 μF) charged in series by an 11 V battery and a resistor (R = 4 Ω) is calculated using the formula T = RC. The equivalent capacitance of the circuit is determined to be approximately 6.3462 μF. The maximum charge on the capacitor is calculated as Q = CV = (6.3462e-6 F)(11 V) = 6.98077e-5 C. The current at maximum is I0 = V/R = 2.75 A, confirming the relationship between voltage, current, and time constant in the charging process.
PREREQUISITES
- Understanding of RC circuits and time constants
- Knowledge of capacitor charging equations
- Familiarity with series and equivalent capacitance calculations
- Basic circuit analysis skills
NEXT STEPS
- Study the derivation of the time constant in RC circuits
- Learn about the behavior of capacitors in series and parallel configurations
- Explore the implications of maximum current (I0) in charging circuits
- Investigate the relationship between voltage, charge, and current in capacitors
USEFUL FOR
Students studying electrical engineering, hobbyists working on circuit design, and anyone looking to deepen their understanding of capacitor behavior in RC circuits.