Help Needed for Solving Electrical Circuit Problem

[lorenz0]

Homework Statement

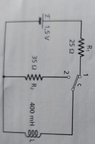
At the beginning the switch c of the circuit is in position 1. At t=0, it switches to position 2.
(1) Find $I(0).$ (2) Find $t*$ such that $I(t*)=35mA.$

Relevant Equations

$I(t)=I(0)(1-e^{(-R/L)t)},\ I(0)=\frac{V}{R}$

What I have done:

(1) $I(0)=\frac{V}{R}=\frac{1.5}{25}A=0.06 A.$

(2) By setting $I(t*)=0.06(1-e^{-(35/0.4)t*})=35 mA$ we get $t*\approx 0.01 s$

What I have done seems correct to me, but the result for part (2) should be different.
I would be grateful if someone could point out to me where I have made a mistake.

 

[kuruman]

You have the wrong expression for $I(t)$. It does not predict that $I(0) =0.06$ A. What is the correct expression to use?

Also, please enter the exponent correctly in LaTeX as e^{-Rt/L} to render as $e^{-Rt/L}$. Or you could write it as $\exp(-R t/L)$.

 

[Steve4Physics]

(2) By setting $I(t*)=0.06(1-e^((-35/0.4)t*))=35 mA$ we get $t*=\approx 0.01 s$

You have used the wrong formula! Can you see why? If you can't, click the spoiler for a hint:

Spoiler

When the switch has been at position 2 for a long time, do you expect the current through the inductor to be 0.06A?

Also, here's a LaTeX formatting hint:
e^(-R/L)t gives: $e^(-R/L)t$ (yuchy)
but
e^{(-R/L)t} gives: $e^{(-R/L)t}$ (slightly yuchy)
Another alternative is:
e^{-(R/L)t} gives: $e^{-(R/L)t}$ (almost not yuchy)

For zero-yuchiness, I would define the time-constant as $\tau = \frac L R$. Then
e^{-\frac t {\tau}} gives: $e^{-\frac t {\tau}}$.

Edit. @kuruman beat me to it or I would not have replied!

 

[lorenz0]

You have the wrong expression for $I(t)$. It does not predict that $I(0) =0.06$ A. What is the correct expression to use?

Also, please enter the exponent correctly in LaTeX as e^{-Rt/L} to render as $e^{-Rt/L}$. Or you could write it as $\exp(-R t/L)$.

I understand now, thanks. It should have been $i(t)=0.06e^{-(R/L)t}$ since, from time $t=0$ onwards, there isn't a battery connected to the "new" circuit anymore. By setting $i(t^*)=35\cdot 10^{-3} A$ I now get the correct value, thanks.