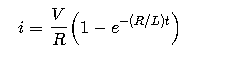Homework Help Overview
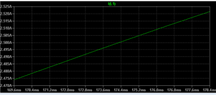
The discussion revolves around determining the time required for the current in an RL circuit to reach 2.5A. The original poster mentions using LTspice for simulation and obtaining a time of approximately 174.38ms, but seeks to calculate it analytically instead.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning
Approaches and Questions Raised
- Participants discuss the relevant equations for current growth in an RL circuit, including Kirchhoff's voltage rule and the relationship between voltage and current in inductors. There are questions about the correctness of the equations used and the meaning of variables within them.
Discussion Status
Participants are actively engaging with the problem, offering guidance on deriving equations and clarifying concepts. There is an emphasis on understanding the underlying principles rather than simply finding a solution. Some participants suggest using simulation tools to visualize the current growth.
Contextual Notes
There are mentions of homework rules requiring an attempt at a solution before receiving help. The original poster has not yet fully learned the differential equations related to the problem, which may affect their ability to calculate the time analytically.