SUMMARY
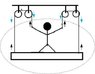
The upward acceleration of a man pulling himself up using two ropes over pulleys is determined to be zero. When the man pulls each rope with a force equal to half his weight (mg/2), the total upward force from the ropes is countered by the combined weight of the man and the platform (2mg). The analysis reveals that the system, consisting of the man and platform, experiences no net force, resulting in zero acceleration. This conclusion is supported by the application of Newton's laws and the understanding of tension in the ropes.
PREREQUISITES
- Understanding of Newton's laws of motion
- Knowledge of tension in ropes and pulleys
- Familiarity with the concept of forces acting on a system
- Basic principles of static and dynamic equilibrium
NEXT STEPS
- Study the principles of tension in static systems
- Learn about the mechanics of pulleys and their applications
- Explore Newton's second law and its implications in dynamic systems
- Investigate the differences between mass and weight in physics
USEFUL FOR
Students of physics, educators teaching mechanics, and anyone interested in understanding forces in pulley systems and static equilibrium.