Find the value of point A and B

[shayaan_musta]

Hello experts.

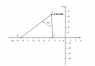
I am attaching the image below. Kindly tell me how to calculate the values of A and B in the given figure?
Now I must find A and B. How to get it?
PS: P=-2.5+4.33i. But A is not at -2.5. Means PA is not making angle 90 with real axis.
Thank you

 

[fresh_42]

One information is missing, either about A or B or another angle. With P and the 55° at P you could still find infinitely many solutions. Or is it supposed to express A as function of B?

 

[shayaan_musta]

No further information is given. Here is the image of the whole page below.
Here is AO=2.38. But how?

 

[Samy_A]

No further information is given. Here is the image of the whole page below.
Here is AO=2.38. But how?

But, as @fresh_42 rightly supposed, you have one more piece of information, namely $\frac {\overline {PA}}{\overline{PB}}=\frac {4.77}{8}$.
Then, as the text suggests, you can calculate A and B using trigonometry.

 

[shayaan_musta]

But how? This is the actual question of mine. For A and B, I posted this thread. If you are saying to solve it myself then what is the cause of posting this thread. Kindly enlighten the way for me to find A and B.

 

[SteamKing]

But how? This is the actual question of mine. For A and B, I posted this thread. If you are saying to solve it myself then what is the cause of posting this thread. Kindly enlighten the way for me to find A and B.

You've been posting information in dribs and drabs, and you are expecting a full solution to what is obviously a much larger problem than just figuring out this triangle.

How about some full disclosure of the complete problem or section from this text you are referencing?

 

[Samy_A]

But how? This is the actual question of mine. For A and B, I posted this thread. If you are saying to solve it myself then what is the cause of posting this thread. Kindly enlighten the way for me to find A and B.

As both @fresh_42 and @SteamKing noted, you first didn't provide enough information to solve the triangle.
From your second attachment we learned that $\frac {\overline {PA}}{\overline{PB}}=\frac {4.77}{8}$

With this information the triangle can be solved.

Now there are probably many ways to do it.
I would begin in the following way:
If $\alpha$ is the angle in A, and $\beta$ the angle in B, $\frac {\sin(\beta)}{\sin(\alpha)}$ can be determined (using $\frac {\overline {PA}}{\overline{PB}}=\frac {4.77}{8}$ and the law of sines).
But we also know that $\alpha+\beta=125°$, so that $\sin(\beta)=\sin(125°-\alpha)=\sin(125°)\cos(\alpha)-cos(125°)\sin(\alpha)$.
These two together will allow to compute $\cot(\alpha)$. And then the other components of the triangle can be computed. It is tedious but it works.

This is just one way to do it. Hopefully someone else will come along with a less tedious method.

As this thread should probably have been posted in the homework section, we are not allowed to give the full solutions.

 

[shayaan_musta]

OK. This is what I did,

sin(125°-α)=sin(125°)cos(α)-cos(125°)sin(α)
since, sin(β)=sin(125°-α)
so,
sin(β)=sin(125°)cos(α)-cos(125°)sin(α)
dividing both sides by sin(α)
so,
sin(β)/sin(α)=sin(125°)cos(α)/sin(α)-cos(125°)sin(α)/sin(α)
sin(β)/sin(α)=sin(125°)cos(α)/sin(α)-cos(125°)
sin(β)/sin(α)=0.8192*cos(α)/sin(α)-(-0.5736)
4.77/8=0.8192*cot(α)+0.5736
0.596=0.8192*cot(α)+0.5736
0.0227=0.8192*cot(α)
cot(α)=0.0227/0.8192
cot(α)=0.028
α=88° and α+β=125° => β=37°
and
AB=sin(P)*PA/sin(β)=6.5

But now what? I still don't have point A coordinates :(

 

[Samy_A]

OK. This is what I did,

sin(125°-α)=sin(125°)cos(α)-cos(125°)sin(α)
since, sin(β)=sin(125°-α)
so,
sin(β)=sin(125°)cos(α)-cos(125°)sin(α)
dividing both sides by sin(α)
so,
sin(β)/sin(α)=sin(125°)cos(α)/sin(α)-cos(125°)sin(α)/sin(α)
sin(β)/sin(α)=sin(125°)cos(α)/sin(α)-cos(125°)
sin(β)/sin(α)=0.8192*cos(α)/sin(α)-(-0.5736)
4.77/8=0.8192*cot(α)+0.5736
0.596=0.8192*cot(α)+0.5736
0.0227=0.8192*cot(α)
cot(α)=0.0227/0.8192
cot(α)=0.028
α=88° and α+β=125° => β=37°
and
AB=sin(P)*PA/sin(β)=6.5

But now what? I still don't have point A coordinates :(

Draw the line from P perpendicular to the horizontal axis. It will cross the horizontal axis in a point Q, just to the left of A.
PAQ is a right triangle and you know the coordinates of P, the coordinates of Q and the angle $\alpha$. That should lead you to the coordinates of A.

 

[shayaan_musta]

Yes, I tried this already before posting post#8 but problem is P has iota in imaginary axis i.e. P(-2.5+4.33i).

 

[SteamKing]

Yes, I tried this already before posting post#8 but problem is P has iota in imaginary axis i.e. P(-2.5+4.33i).

I don't know what more you want.
So far:
1. You have determined all three angles in this triangle
2. You have calculated the length of one side of this triangle.
3. You know the coordinates of one of the vertices of this triangle.

It's time to let loose on the trigonometry and find the rest of the missing information.

Hint: Use the Law of Sines to find the lengths of the other two sides.

 

[shayaan_musta]

OK

 

[Samy_A]

Yes, I tried this already before posting post#8 but problem is P has iota in imaginary axis i.e. P(-2.5+4.33i).

You lost me there.

In triangle APQ:
$\cot(\alpha)=\frac {|AQ|}{|PQ|}$. The only unknown here is $|AQ|$.
Thus:
$|AQ|=\cot(\alpha)*|PQ|=0.028*4.33=0.12$
So the coordinates of A are: $(-2.5+0.12,0)=(-2.38,0)$

For B (same as above, but now in the right triangle BPQ):
$\beta=\pi-55*\frac{\pi}{180}-1.543=0.638$ (in radians).
$|BQ|=\cot(\beta)*|PQ|=\cot(0.638)*4.33=1.349*4.33=5.84$
So the coordinates of B are: $(-2.5-5.84,0)=(-8.34,0)$

 

[shayaan_musta]

Best Regards,
Pinky