anemone
Gold Member
MHB
POTW Director
- 3,851
- 115
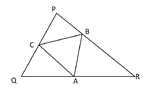
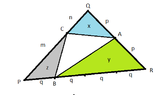
In triangle $PQR$, the points $A,\,B,\,C$ lie on the line segments $QR$, $RP$ and $PQ$ respectively, such that $A$ is the midpoint of $QR$, $RB=3BP$ and $\dfrac{PC}{CQ}=\dfrac{m}{n}$. If $y$ is the area of triangle $RAB$, $x$ is the area of triangle $AQC$ and $z$ is the area of triangle $PCB$, and $x^2=yz$, find the value of $\dfrac{m}{n}$.