Find the value of the trigonometric sum
- Thread starter Amlan mihir
- Start date
Click For Summary
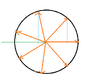
The discussion focuses on solving a trigonometric sum involving angles derived from the unit circle. Participants suggest using the sine and cosine functions, specifically leveraging the identity sin(α)cos(β) = 1/2 (sin(α + β) + sin(α - β) to simplify the expression. By selecting α as π/7 and applying product-to-sum conversions, the result simplifies to -1/2. Additionally, the symmetry of the unit circle with seven vectors, each separated by an angle of 2π/7, confirms that the sum of the cosine components equals zero, leading to the conclusion that cos(θ) + cos(2θ) + cos(3θ) = -1/2.
PREREQUISITES- Understanding of trigonometric identities, particularly product-to-sum formulas.
- Familiarity with the unit circle and its properties.
- Knowledge of sine and cosine functions and their behavior at specific angles.
- Basic algebraic manipulation skills for simplifying trigonometric expressions.
- Study trigonometric identities, focusing on product-to-sum conversions.
- Explore the properties of the unit circle and symmetrical vectors in trigonometry.
- Learn about the implications of angle symmetry in trigonometric functions.
- Practice solving similar trigonometric sums using various angles and identities.
Students and educators in mathematics, particularly those studying trigonometry, as well as anyone interested in advanced problem-solving techniques involving trigonometric sums.
Similar threads
- · Replies 6 ·
- · Replies 6 ·
- · Replies 14 ·
- · Replies 9 ·
- · Replies 4 ·
- · Replies 25 ·
- · Replies 6 ·
- · Replies 6 ·