MHB Find the value of X in terms of Y

  • Thread starter Thread starter mathlearn
  • Start date Start date
  • Tags Tags
    Terms Value
Click For Summary
SUMMARY

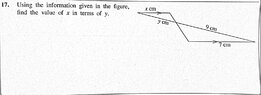
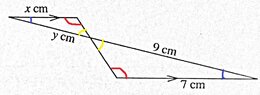
The discussion focuses on finding the value of X in terms of Y using the properties of similar triangles. The relationship established is based on the ratio of the sides facing equal angles, represented by the equation $\frac{7}{X} = \frac{9}{Y}$. This leads to the conclusion that $7Y = 9X$, which simplifies to $X = \frac{7Y}{9}$. Additionally, the importance of distinguishing between lowercase and uppercase letters in mathematical notation is emphasized.

PREREQUISITES
  • Understanding of similar triangles and their properties
  • Basic algebraic manipulation skills
  • Familiarity with mathematical notation
  • Knowledge of ratios and proportions
NEXT STEPS
  • Study the properties of similar triangles in geometry
  • Practice solving equations involving ratios
  • Explore the significance of notation in mathematical expressions
  • Learn more about algebraic expressions and their simplifications
USEFUL FOR

Students studying geometry, mathematics educators, and anyone interested in mastering the concepts of ratios and similar triangles.

mathlearn
Messages
331
Reaction score
0

Attachments

  • tri_similar.jpg
    tri_similar.jpg
    112.9 KB · Views: 91
  • tri_similar2.jpg
    tri_similar2.jpg
    46.5 KB · Views: 85
Last edited by a moderator:
Mathematics news on Phys.org
mathlearn said:
All I see is the three angles of the triangles equal.
In this case the triangles are similar.
 
Evgeny.Makarov said:
In this case the triangles are similar.

As said above,

In similar triangles, the sides facing the equal angles are always in the same ratio

$\frac{7}{X}$ = $\frac{9}{Y}$

$7Y$ = $9X$

Correct I guess?

Many Thanks :)
 
mathlearn said:
$7Y$ = $9X$
Correct, but the final answer is $x=7y/9$ ("find the value of $x$ in terms of $y$").

Also, in mathematics lowercase and uppercase letters often denote different objects, so they should not be mixed.
 
Sure :) Thank you for the advice :)

Many Thanks :)
 

Similar threads

High School Why does the trigonometry of obtuse angles use ref angles?
  • · Replies 10 ·
Replies
10
Views
2K
MHB Can You Find the Angle in This Isosceles Triangle Problem?
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Method for finding a complex series?
  • · Replies 10 ·
Replies
10
Views
2K
MHB Find the value of x square + y square
  • · Replies 2 ·
Replies
2
Views
15K
Undergrad Help with area formula using direction cosines
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Finding the inverse tangent of a complex number
  • · Replies 3 ·
Replies
3
Views
3K
MHB Finding minimum value of function with two variable
  • · Replies 7 ·
Replies
7
Views
3K
MHB Is this Trigonometric Expression a Constant Function of x?
  • · Replies 2 ·
Replies
2
Views
1K
MHB Solve for the angles in a triangle
  • · Replies 4 ·
Replies
4
Views
2K
Undergrad ##x\lt y \lt z## positive integer numbers and if ##\dfrac 1x+\dfrac 1y+\dfrac 1z=\dfrac 13##
  • · Replies 6 ·
Replies
6
Views
2K