Discussion Overview
The discussion revolves around calculating the volume of a solid using both the shell and disk methods in calculus. Participants are exploring the integration techniques involved and addressing specific calculations related to the volume formula.
Discussion Character
- Mathematical reasoning, Homework-related
Main Points Raised
- One participant expresses difficulty in obtaining the correct answer for the volume calculation.
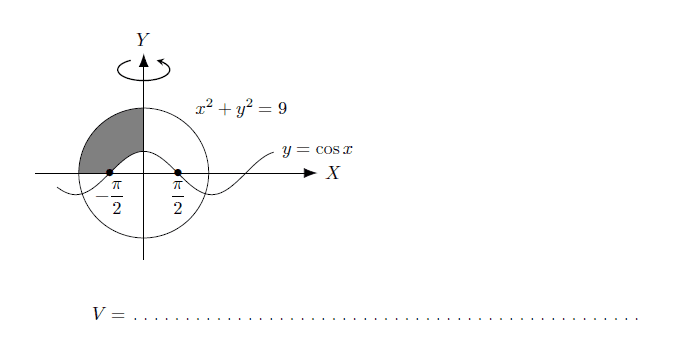
- Another participant presents a volume expression involving integrals, specifically $\displaystyle V = 18\pi - 2\pi \int_0^{\pi/2} x \cos{x} \, dx$ and $\displaystyle V = 18\pi - \pi \int_0^1 [\arccos{y}]^2 \, dy$.
- A subsequent post repeats the volume expression and questions the origin of the term $18\pi$.
- Another participant provides a formula for the volume of a hemisphere, $\dfrac{2\pi r^3}{3}$, specifying $r = 3$, which may relate to the $18\pi$ term.
Areas of Agreement / Disagreement
Participants are seeking clarification on the calculations, particularly the origin of the $18\pi$ term, indicating that there is no consensus on this aspect yet.
Contextual Notes
The discussion includes unresolved mathematical steps regarding the integration and the specific calculations leading to the volume expression.