Find the weight of a partially submerged cylinder

[Richie Smash]

Homework Statement

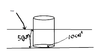
Hello, there is a cylinder with cross sectional area 10cm².
The cylinder has a length of 50cm partially submerged in water and floats upright.
Taking acceleration due to gravity as 10 m s^-2 and the density of water to be 1000 kg m^-3
Find the weight of the cylinder using archimedes principle.

Homework Equations

Upthrust = volume *density *gravity
Upthrust = mass of water displaced *gravity

The Attempt at a Solution

So, I found the volume of the part of the cylinder that is submerged by multiplying the cross sectional area by 50cm and got 500cm³

From here I converted that that to metres and then used the formula for upthrust involving density and gravitational acceleration and I got 0.05 N

Now I use the knowledge that the upthrust = mass of water displaced * gravity

so 0.05N= Mw*10
Mw= 0.05/10
Mw = 0.005Kg

So now know the mass for that part of the cylinder, but the problem is they didnt inform me of what fraction was submerged, so I don't know how to find the mass for the whole thing.

If I did I would use F=ma and solve.

 

[lekh2003]

I think this is a statics problem. You need to find the point at which the buoyancy is equal to weight of the cylinder. There has to be a sweet spot where the cylinder is not going up or down.

 

[haruspex]

The cylinder has a length of 50cm partially submerged

I gather you mean that it has unknown length, but 500cm of it is submerged.

I got 0.05 N

Doesn't seem enough. Check that.

Now I use the knowledge that the upthrust = mass of water displaced * gravity

You already used that. What else must the upthrust equal to achieve steady state?

 

[Richie Smash]

The question says that yes the height is unknown but 50 cm is submerged, not 500.

Well to figure out that value I multipled the height that do know, 50cm, by the cross sectional area, giving me 500cm cubed.

I converted that to metres then used the upthrust formula, so did get that tiny value, but its only for piece of the cylinder

 

[lekh2003]

The question says that yes the height is unknown but 50 cm is submerged, not 500.

Well to figure out that value I multipled the height that do know, 50cm, by the cross sectional area, giving me 500cm cubed.

I converted that to metres then used the upthrust formula, so did get that tiny value, but its only for piece of the cylinder

I stand by saying that whatever the buoyant force is, the entire weight of the cylinder. Set a variable and solve for the entire weight, then you wil know all the details.

I got 0.05 N

And be careful when converting units when the units are cubed.

 

[haruspex]

50 cm is submerged, not 500.

Sorry, typo.

I converted that to metres then used the upthrust formula, so did get that tiny value, but its only for piece of the cylinder

Yes, but I am querying the accuracy of that calculation. Please show the details.

You did not answer this question:

What else must the upthrust equal to achieve steady state?

 

[Richie Smash]

The upthrust must also equal to the volume of water displaced, my calucation was this, 10cm² is 0.001m²
Multiply that by 50 cm or 0.05 m and you will get 0.0005 so multiply that by 1000 you get 0.5 multiply by 10 you get 5

SO the upthrust is actually 5 Newtons and I'm guessing the volume is 5mcubed for that part of the clinder

 

[lekh2003]

50 cm or 0.05 m

50 cm is 0.5 m

 

[Richie Smash]

yes sorry typo

 

[haruspex]

I'm guessing the volume is 5mcubed for that part of the clinder

You already calculated the volume to find the weight of water displaced, and hence the upthrust.
What else must the upthrust equal for the system to be in equilibrium?

 

[Richie Smash]

I'm afraid I'm unsure, perhaps the mass?

 

[lekh2003]

yes sorry typo

First of all, not a typo. You made an error in the entire calculation because of that.

I'm afraid I'm unsure, perhaps the mass?

Second, I have literally told you and @haruspex has repeatedly hinted at it, but you yet keep asking the same question.

 

[haruspex]

I'm afraid I'm unsure, perhaps the mass?

What are the forces on the cylinder?

 

[Richie Smash]

The forces on the cylinder are the force of grvity acting upon it, and the upthrust.

Also I am sure I fixed this calculation now, it should be 50N is the upthrust

 

[haruspex]

The forces on the cylinder are the force of grvity acting upon it, and the upthrust.

So what equation can you write?

 

[Richie Smash]

I included a diagram here.

The equation I can write is

Mass x gravity = volume * density*gravity

However as you can see in the diagram, this would only be for the section of the cylinder underwater, my problem all along is how do I know figure out the weight, or mass or volume whichever one of the rest on top, because according to my calculation the upthrust is only equal to that section of the cylinder, and my thinking is, I need the height of the entire thing because I only calculated the volume of one section of the cylinder, but they don't give any fractions or hints in this question.

 

[haruspex]

The equation I can write is

Mass x gravity = volume * density*gravity

No, just an equation connecting the forces on the cylinder.

 

[Richie Smash]

Ok it will be,

Fb=mg

 

[lekh2003]

Ok it will be,

Fb=mg

It is however the force of buoyancy (which is only on part of the cylinder) compared to the $mg$ which is of the whole cylinder.

 

[haruspex]

So put it all together:

Find the weight of the cylinder

50N is the upthrust

Fb=mg

 

[SammyS]

Homework Statement

Hello, there is a cylinder with cross sectional area 10cm².
The cylinder has a length of 50cm partially submerged in water and floats upright.
Taking acceleration due to gravity as 10 m s^-2 and the density of water to be 1000 kg m^-3
Find the weight of the cylinder using Archimedes Principle.
2. Homework Equations
...

Please state Archimedes Principle .

 

[Richie Smash]

Archimedes principle states that the upthrust on a partially or fully submerged object in a fluid is equal to the weight of the fluid that is displaced.
Well I can figure out that using
Fb=mg

The mass of the cylinder I have found would be 5kg. I know I'm missing something vital here... but it just is not adding up to me.

As Lekh stated in this equation, the ''Fb'' term would be the force only on part of the cylinder, so using the formula, would the 5kg mass I have computed = to the entire mass or just part of the mass, if it the entire mass then problem solved but if not...

 

[haruspex]

Well I can figure out that using
Fb=mg

That is ambiguous because there are two masses.

To be clear, you successfully used Archimedes' principle (some numerical errors aside) to arrive at
Fb = m_{water displaced} g

The equation it took so long to add was Newton's ΣF=ma:

Fb - m_{floating object} g = 0

The mass of the cylinder I have found would be 5kg

Yes, but you are asked for the weight, not the mass.

 

[Richie Smash]

SO the weight is 50N?

 

[lekh2003]

SO the weight is 50N?

Assuming the mass is $5 kg$ and the acceleration due to gravity is $10m/s^2$

 

[lekh2003]

Units?

Sorry, I fixed it.