Find Time Constant for RC Circuit: Solve the Equation!

Click For Summary
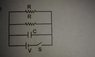
SUMMARY

The time constant for an RC circuit is defined by the equation τ = R_eq C, where R_eq is the equivalent resistance. In this discussion, R_eq is calculated as R/2, leading to an initial conclusion of t = RC/2. However, it is established that once the switch is closed, all components are in parallel, resulting in an immediate potential across the capacitor, which leads to a time constant of 0 due to the ideal voltage source and negligible wire resistance.

PREREQUISITES
  • Understanding of RC circuit theory
  • Familiarity with the concept of time constant in electrical circuits
  • Knowledge of parallel circuit rules
  • Basic principles of ideal voltage sources
NEXT STEPS
  • Study the implications of ideal voltage sources on circuit behavior
  • Learn about the characteristics of parallel circuits in depth
  • Explore the derivation and applications of the time constant in various RC configurations
  • Investigate the effects of non-ideal components on time constants in circuits
USEFUL FOR

Electrical engineering students, educators teaching circuit theory, and professionals working with RC circuits and time constant calculations.

utkarshakash
Gold Member
Messages
852
Reaction score
13

Homework Statement


The time constant of charging for the capacitor shown in the figure is


Homework Equations



See attached diagram

The Attempt at a Solution



\tau = R_{eq} C

R_{eq} = R/2

So the answer should be t= RC/2. But the correct answer is 0! :confused:
 

Attachments

  • 20140422_214153.jpg
    20140422_214153.jpg
    14.8 KB · Views: 482
Physics news on Phys.org
Once the switch is closed all the components are in parallel, right? What's the rule for the potential across components in parallel?
 
gneill said:
Once the switch is closed all the components are in parallel, right? What's the rule for the potential across components in parallel?

They all have the same potential difference.
 
utkarshakash said:
They all have the same potential difference.

Right. And if the voltage source is ideal and the wires have entirely negligible resistance, then the capacitor voltage immediately after the switch closes must be...
 
gneill said:
Right. And if the voltage source is ideal and the wires have entirely negligible resistance, then the capacitor voltage immediately after the switch closes must be...

It should be V. Thus time constant must be 0. Thanks !
 

Thread 'Magnitude of buoyant force in fluids of different densities'

The book claims the answer is that all the magnitudes are the same because "the gravitational force on the penguin is the same". I'm having trouble understanding this. I thought the buoyant force was equal to the weight of the fluid displaced. Weight depends on mass which depends on density. Therefore, due to the differing densities the buoyant force will be different in each case? Is this incorrect?
View full post »

Similar threads

Current through an inductor as a function of time
  • · Replies 10 ·
Replies
10
Views
895
How to find the equivalent resistance of this infinite circuit?
  • · Replies 10 ·
Replies
10
Views
3K
Finding Current in Resistors & Charge of Capacitor
  • · Replies 4 ·
Replies
4
Views
2K
Time constant for parallel RC circuit
  • · Replies 2 ·
Replies
2
Views
2K
Capacitor circuit time constant problem
  • · Replies 2 ·
Replies
2
Views
2K
Basic RC Circuit Homework: Calculate Time Constant & Charge Decay
  • · Replies 3 ·
Replies
3
Views
2K
Why can we add impedances in series?
  • · Replies 4 ·
Replies
4
Views
2K
Find the time constant of the circuit
  • · Replies 1 ·
Replies
1
Views
1K
RC Multiloop Circuits, Find Current at Specific Time
  • · Replies 9 ·
Replies
9
Views
2K
Time for capacitor charging in RLC circuit.
  • · Replies 3 ·
Replies
3
Views
3K