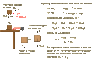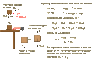Find work given a pulley and two weights

[fishturtle1]

Homework Statement

Problem 6.65
Two blocks are connected by a very light string passing over a massless and frictionless pulley (Figure (Figure 1) ). The 20.0-N block moves 75.0 cm to the right and the 12.0-N block moves 75.0 cm downward.

Question: Find the total work done on 20.0-N block if there is no friction between the table and the 20.0-N block.

Homework Equations

ΣF = ma
Wtotal = F * s cos(φ), where the force is constant.
Wtotal = 1/2(m)vf^2 - 1/2(m)vi^2
vf^2 = vi^2 + 2ad

The Attempt at a Solution

So I started with the 12.0N weight.

ΣF = m1a = T - 12.0N, where m1 is the mass of the 12.0N weight. I also say acceleration is the same for both weights because they are in the same system.

then T = (12/9.8)a+12.0N

Then I set up my force equation for the 20.0N weight.

ΣF = m2a = T, where m2 = 20/9.8

(20/9.8)a = (12/9.8)a + 12.0N
(8/9.8)a = 12.0N
a = 14.7 m/s^2

Then I plug this into my equation for tension.

T = (12/9.8)14.7 + 12.0
T=18+12.0
T=30N

Then W = T * s cos(0°)
W = (30)(.75)(1) = 22.5 J.

Which is wrong.

2nd attempt

I thought maybe force is not constant, although I'm not sure why it wouldn't be. SO i used this equation.

W = 1/2(m)vf^2 - 1/2(m)vi^2, where i assume vi = 0m/s
then
W = 1/2(m)vf^2

to solve for vf: vf^2 = vi^2 +2ad
vf^2 = 2(14.7)(.75)
vf^2 = 22.05

Then
W = 1/2(20)(22.05)
W = 220.5J

which is also wrong. I know my displacement vector is correct so it must be my acceleration but I can't see anywhere that i made an error in calculating it.

 

[BvU]

Hi,

I take it figure 1 is like here ?

Check a

 

[haruspex]

The question statement is unclear. Are we to assume that the blocks are released from rest, so they will accelerate in the obvious way, but you are just to find the work done over the first 75cm of movement?

m1a = T - 12.0N,

Looks like you are defining positive up, so a is expected to be negative.

m2a = T,

But now a needs to be positive.

 

[fishturtle1]

Hi,

I take it figure 1 is like here ?

Check a

Yes that is the figure, sorry i forgot to add it. I'll add it now. Never mind i waited too long to edit. But yes that is the figure.

 

[fishturtle1]

The question statement is unclear. Are we to assume that the blocks are released from rest, so they will accelerate in the obvious way, but you are just to find the work done over the first 75cm of movement?

Looks like you are defining positive up, so a is expected to be negative.

But now a needs to be positive.

I am unsure if we are supposed to assume the blocks start from rest. I think what that means is the initial velocity and final velocity aren't needed to solve this problem.

I also did away with my original equations for tension after looking at http://hyperphysics.phy-astr.gsu.edu/hbase/hpul2.html. This website had a formula for tension which was a = [(mass of 12.0N weight)(g) - μ(mass of 20.0N weight)(g)]/(mass of 12.0N + mass of 20.0N). I used this to solve for acceleration. Then plugged that acceleration in for :

ΣF = (mass of 20.0N)(a) = T,
(20/9.8)(3.675) = T,
T = 7.501

Then i plugged this force into my work equation:

W = F * s cos(Φ)
W = 7.501 * .75 * 1 = 5.63J. This came up as the correct answer.But I'm stuck on how we used the original equation to find acceleration.

Their vector equation, I assume, looked like this:

ΣF = (m1 + m2)a = w2 - ƒ - T2 + T1, where T1 = T2.

so my confusion is this: I was under the impression you could only use Newton's second law for one object at a time. So in this case are we just setting up a Newton's second law equation twice and then combining them?

No friction.
1st weight: ΣF = m1a = T
2nd weight: ΣF = m2a = w2 - T,
Then their sum would be: m1a + m2a = w2 - T + T => (m1 + m2)a = w2 = > a = w2/(m1+m2).

I guess this is the first time I've seen this happen so I'm not sure if this is the calculations made.

 

[haruspex]

are we just setting up a Newton's second law equation twice and then combining them?

Yes, you can get the same equation by doing that.
As I hinted before, you had a sign error in your original equations. I cannot say exactly where the error was, just that the equations were inconsistent.

 

[fishturtle1]

Yes, you can get the same equation by doing that.
As I hinted before, you had a sign error in your original equations. I cannot say exactly where the error was, just that the equations were inconsistent.

ok. Thank you for your help! I will do some more two weights/one pulley problems to make sure i got it