Finding $a$ for a Degenerate BFS in Given System of Restrictions

[I like Serena]

Don't we also have to check the case where we have the following tableau:

$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & \theta & \\
P_3 & 4-\frac{6}{a} & 1-\frac{2}{a} & 0 & 1 & 0 & -\frac{2}{a} & & L_1'=L_1-2L_3'\\ \\
P_4 & 2-\frac{3}{a} & 2-\frac{1}{a} & 0 & 0 & 1 & -\frac{1}{a} & & L_2'=L_2-L_3'\\ \\
P_2 & \frac{3}{a} & \frac{1}{a} & 1 & 0 & 0 & \frac{1}{a} & & L_3'=\frac{L_3}{a}
\end{matrix}$

where $a> \frac{3}{2}$

and we choose $P_1$ to get in the basis instead of $P_5$ ?

Ah, did we miss that one?
Yes, we should also check that one. (Nod)

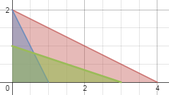
The corresponding graph is:
View attachment 5111
The tableau corresponds to the intersection of the green line with the y-axis.
If we bring in $P_1$ and leave $P_3$, we move to the intersection of the blue line with the green line. (Nerd)
Hmm... didn't we already do that? (Wondering)

 

[evinda]

Ah, did we miss that one?
Yes, we should also check that one. (Nod)

Then we get the following tableau, right?
$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & & \theta & \\
P_3 & \frac{6a-9}{2a-1} & 0 & 0 & 1 & \frac{2-a}{2a-1} & \frac{3}{1-2a} & & &L_1''=L_1'-\left( 1-\frac{2}{a} \right )L_2'' \\ \\
P_1 & \frac{2-\frac{3}{a}}{2-\frac{1}{a}} & 1 & 0 & 0 & \frac{1}{2-\frac{1}{a}} & \frac{1}{1-2a} & & & L_2''=\frac{L_2'}{2-\frac{1}{a}}\\ \\
P_2 & \frac{4}{2a-1} & 0 & 1 & 0 & \frac{1}{1-2a} & \frac{2}{2a-1} & & &L_3''=L_3'-\frac{1}{a}L_2''
\end{matrix}$

This gives a non-degenerate basic feasible solution so we have to continue the algorithm. Right? (Thinking)

Hmm... didn't we already do that? (Wondering)

Did we? At which point? (Thinking)

 

[I like Serena]

Then we get the following tableau, right?
$\begin{matrix}
B & b & P_1 & P_2 & P_3 & P_4 & P_5 & & \theta & \\
P_3 & \frac{6a-9}{2a-1} & 0 & 0 & 1 & \frac{2-a}{2a-1} & \frac{3}{1-2a} & & &L_1''=L_1'-\left( 1-\frac{2}{a} \right )L_2'' \\ \\
P_1 & \frac{2-\frac{3}{a}}{2-\frac{1}{a}} & 1 & 0 & 0 & \frac{1}{2-\frac{1}{a}} & \frac{1}{1-2a} & & & L_2''=\frac{L_2'}{2-\frac{1}{a}}\\ \\
P_2 & \frac{4}{2a-1} & 0 & 1 & 0 & \frac{1}{1-2a} & \frac{2}{2a-1} & & &L_3''=L_3'-\frac{1}{a}L_2''
\end{matrix}$

This gives a non-degenerate basic feasible solution so we have to continue the algorithm. Right? (Thinking)

I don't think that is a feasible solution for $a > \frac 32$.
Instead I think we should move to the basis $P_1, P_2, P_4$. (Thinking)

Did we? At which point? (Thinking)

Turns out we covered basis $P_2, P_3, P_4$ in post #7.
But I can't find basis $P_1, P_2, P_4$. (Nerd)

 

[evinda]

I don't think that is a feasible solution for $a > \frac 32$.

Why isn't it feasible? Aren't all the components positive? (Thinking)

$a> \frac{3}{2} \Rightarrow 2a>3 \Rightarrow 6a>9$

$2a>3 \Rightarrow 2a>1$

$\frac{2-\frac{3}{a}}{2-\frac{1}{a}}=\frac{2a-3}{2a-1}>0$

 

[I like Serena]

Why isn't it feasible? Aren't all the components positive? (Thinking)

$a> \frac{3}{2} \Rightarrow 2a>3 \Rightarrow 6a>9$

$2a>3 \Rightarrow 2a>1$

$\frac{2-\frac{3}{a}}{2-\frac{1}{a}}=\frac{2a-3}{2a-1}>0$

It shouldn't be feasible since it corresponds to the intersection of the red line (non-basic variable $P_4$)[/color] and the green line (non-basic variable $P_5$)[/color].
https://www.physicsforums.com/attachments/5111
When $a > \frac 32$ that intersection should have either $x_2 < 0$ or $x_1 < 0$.

 

[evinda]

It shouldn't be feasible since it corresponds to the intersection of the red line (non-basic variable $P_4$)[/color] and the green line (non-basic variable $P_5$)[/color].

When $a > \frac 32$ that intersection should have either $x_2 < 0$ or $x_1 < 0$.

So have I done something wrong at the calculations? (Thinking)Which $a$ did you pick to draw the third inequality?

 

[I like Serena]

So have I done something wrong at the calculations? (Thinking)Which $a$ did you pick to draw the third inequality?

I picked $a=3$.
Oh wait. (Wait)
It's the intersection of the blue line (non-basic variable $P_4$)[/color] and the green line (non-basic variable $P_5$)[/color].
I made a mistake. (Blush).

 

[evinda]

It's the intersection of the blue line (non-basic variable $P_4$)[/color] and the green line (non-basic variable $P_5$)[/color].
I made a mistake. (Blush).

So we have to continue the algorithm, picking either the column $P_4$ or the column $P_5$, right?

 

[evinda]

If we choose $P_4$ to get in the basis we have to distinguish the cases:

• $a \leq 2$ and
• $a>2$

Right? (Thinking)

 

[evinda]

One way to find it, is to make a drawing, which will reveal where and when degeneracy can happen.

Could you explain further to me how we can find from a drawing all the possible degenerate basic feasible solution although we don't have a specific value of $a$ ? (Thinking)

 

[I like Serena]

Could you explain further to me how we can find from a drawing all the possible degenerate basic feasible solution although we don't have a specific value of $a$ ? (Thinking)

Every point on the boundary of the feasible region where 3 or more lines intersect is a degenerate basic feasible solution.
When we get to such a point with the simplex method, we won't be able to tell in which direction to continue. (Nerd)

This is already the case in $(0,2)$, although it still depends on $a$ whether that is actually a feasible solution.
Actually, for $a=0$ we would also get degenerate basic feasible solutions. (Nerd)

 

[evinda]

Every point on the boundary of the feasible region where 3 or more lines intersect is a degenerate basic feasible solution.

Why is it like that? (Thinking)

When we get to such a point with the simplex method, we won't be able to tell in which direction to continue. (Nerd)

You mean that there will be more than one possibilities to check? (Thinking)

This is already the case in $(0,2)$, although it still depends on $a$ whether that is actually a feasible solution.
Actually, for $a=0$ we would also get degenerate basic feasible solutions. (Nerd)

How do we find $(0,2)$ ?

Also if we pick a specific $a$ and find the points on the boundary will we find all the possible degenerate basic feasible solutions?
i.e. if we pick a different one will we find the same points? (Thinking)

 

[evinda]

So we have to continue the algorithm, picking either the column $P_4$ or the column $P_5$, right?

If we pick $P_4$ to get in the basis, then if $a \leq 3$ $P_2$ will get out of the basis. Otherwise $P_3$ gets out of the basis. Right? (Thinking)