Finding a new way to calculate one side of a triangle

[nearc]

hopefully this is the right place for this question, the first part is a trig/geometry question but it is really a integration question:

i'm trying to find another way to compute d1 without using law of cosines because i don't know how to integrate (cos a)^.5, if someone knows how to do that please let me know.

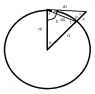
in the figure provided I'm attempting to find d1 as a function of angle a, r0 and r1 are constants and angles t, p and lengths d0, x can be computed trivially.

i can use law of sines to find d1 if i can make b, m or c a function of a

 

[Simon Bridge]

...r0 and r1 are constants...

If r1=r0+x, then d1 is related to r0 and r1 by pythagoras.

 

[SteamKing]

This diagram is a handy way to visualize the relationship between the trig functions and the angle using a unit circle: (credit: wikipedia)

 

[nearc]

If r1=r0+x, then d1 is related to r0 and r1 by pythagoras.

yes, r1=r0+x, but there are no right angles in the figure

 

[nearc]

This diagram is a handy way to visualize the relationship between the trig functions and the angle using a unit circle: (credit: wikipedia)

thanks i'll reflect on this, but i suspect that this would only be useful in the case where i have right angles

 

[Simon Bridge]

yes, r1=r0+x, but there are no right angles in the figure

Ah - so d1 is not a tangent ... it looks a lot like it is supposed to be one in the figure.

This is where I suspect you need to look for another way to set up the integral - or learn to use elliptic integrals.

 

[nearc]

Ah - so d1 is not a tangent ... it looks a lot like it is supposed to be one in the figure.

This is where I suspect you need to look for another way to set up the integral - or learn to use elliptic integrals.

can you give me some good lead for elliptic integrals? thansk

 

[Simon Bridge]

$$\int \cos^{\frac{1}{2}}\!(x)\; dx = 2E\big(\frac{x}{2}\big|2\big)$$

$E(x|m)$
Elliptic Integral of the seconds kind [properties]

 

[nearc]

$$\int \cos^{\frac{1}{2}}\!(x)\; dx = 2E\big(\frac{x}{2}\big|2\big)$$

$E(x|m)$
Elliptic Integral of the seconds kind [properties]

thanks for your help, but I've looked through some basic elliptical integrals and I'm not finding anything like (cos x)^.5 the basic form is 1-(sin x )^2

also what I'm working with is not an ellipse it is a circle. the difference is that instead of a constant radius from the center tracing out the circle it is circle traced from a point off center and instead of a constant radius length the this segment length changes

 

[Simon Bridge]

"elliptic integral" not "elliptical".
It is the name for a class of functions - they have application beyond elliptic curves.

How about:
http://integrals.wolfram.com/index.jsp?expr=sqrt(cos(x))&random=false

Um - note: if x is very small compared with r0, then cos(m)~1 and sin(m)~m and tan(m)~m.

In the diagram in post #3 - your triangles are AOD and ADE.
The exsec side is you side x.
AO=OD=r0
AD=d0
... like that.

 

[nearc]

thanks to simon I've figured out the simple elliptic however i now have a more difficult version:

$$\int_0^{2 \pi } \sqrt{\left(1-\frac{60}{61} \cos (x-179)\right) \left(1-\frac{60}{61} \cos (x-t)\right)} \, dx $$

using mathematica i can find the solution to

$$\int \sqrt{1-\frac{60}{61} \cos (x-t)} \, dx $$

but mathematica was not able to solve the harder version, any ideas?

also how do get the latex to show correctly?

thanks mark44

 

[Mark44]

thanks to simon I've figured out the simple elliptic however i know have a more difficult version:

\int_0^{2 \pi } \sqrt{\left(1-\frac{60}{61} \cos (x-179)\right) \left(1-\frac{60}{61} \cos (x-t)\right)} \, dx

using mathematica i can find the solution to

\int \sqrt{1-\frac{60}{61} \cos (x-t)} \, dx

but mathematica was not able to solve the harder version, any ideas?

also how do get the latex to show correctly?

Add $$[/color] before and after your LaTeX. Here's what your stuff looks like with this addition.
$$\int_0^{2 \pi } \sqrt{\left(1-\frac{60}{61} \cos (x-179)\right) \left(1-\frac{60}{61} \cos (x-t)\right)} \, dx $$

$$\int \sqrt{1-\frac{60}{61} \cos (x-t)} \, dx
$$

 

[Simon Bridge]

$$\left(1-\frac{60}{61} \cos (x-179)\right) \left(1-\frac{60}{61} \cos (x-t)\right)$$ ... hmmm? expand the brackets and try trig identities?
A quick path can be to expand the trig function by the Euler relations since manipulating exponentials is usually easier.

 

[nearc]

thanks simon, are you referring to

$$e^{\text{ix}}=x \cos + i x \sin $$

 

[Simon Bridge]

thanks simon, are you referring to

$$e^{\text{ix}}=x \cos + i x \sin $$

That does not make any sense!
You mean:
$$e^{\text{ix}}=\cos(x) + i \sin(x) $$... then yes
http://en.wikipedia.org/wiki/Euler's_formula

 

[nearc]

yep that's it, mathematica likes to switch things?

 

[Simon Bridge]

Dunno - never used mathematica.