nearc
Gold Member
- 65
- 6
hopefully this is the right place for this question, the first part is a trig/geometry question but it is really a integration question:
i'm trying to find another way to compute d1 without using law of cosines because i don't know how to integrate (cos a)^.5, if someone knows how to do that please let me know.
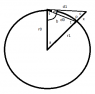
in the figure provided I'm attempting to find d1 as a function of angle a, r0 and r1 are constants and angles t, p and lengths d0, x can be computed trivially.
i can use law of sines to find d1 if i can make b, m or c a function of a
i'm trying to find another way to compute d1 without using law of cosines because i don't know how to integrate (cos a)^.5, if someone knows how to do that please let me know.
in the figure provided I'm attempting to find d1 as a function of angle a, r0 and r1 are constants and angles t, p and lengths d0, x can be computed trivially.
i can use law of sines to find d1 if i can make b, m or c a function of a
Attachments
Last edited: