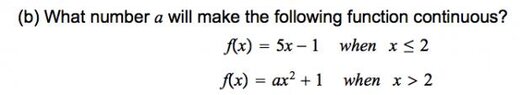Finding a value that will make a function continuous

Click For Summary
SUMMARY

The discussion centers on determining the value of 'a' that ensures the continuity of a function at x=2. The equation 5(2)-1 = a(2)^2 + 1 is established as the condition for continuity, leading to the solution a = 2. The participants clarify that for a function to be continuous at a specific point, the left-hand limit and the function value must be equal at that point. This understanding is crucial for ensuring the function behaves predictably around x=2.

PREREQUISITES
  • Understanding of continuous functions in calculus
  • Familiarity with limits and their properties
  • Basic algebra skills for solving equations
  • Knowledge of function notation and evaluation
NEXT STEPS
  • Study the concept of limits in calculus
  • Learn about the definition of continuity in mathematical functions
  • Explore piecewise functions and their continuity conditions
  • Investigate the implications of discontinuities in real-world applications
USEFUL FOR

Students in calculus, mathematics educators, and anyone interested in understanding the principles of function continuity and its applications in various mathematical contexts.

shle
Messages
4
Reaction score
0
Hi All, just a question regarding continuous functions.
From what I understand if x > 2, then any value of 'a' should make this function continuous? Any clarification would be very helpful!
Thanks in advance!
 

Attachments

  • 2b.jpg
    2b.jpg
    8.8 KB · Views: 79
Physics news on Phys.org
Try 5(2)-1 = a(2)^2+1 solve for a
 
Thank you, I get a = 2. Can you please explain to me the intuition behind that? Why is it that I have to use 5(2)-1 = a(2)^2+1 and solve for a?
 
For the function to be continuous at x=2, then they must be equal at that point.
 

Similar threads

Undergrad Continuity of Quotient of Complex Values
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Naming convention for "Functional Variance"?
  • · Replies 7 ·
Replies
7
Views
2K
High School Finite linear combination of continuous functions is continuous?
  • · Replies 3 ·
Replies
3
Views
1K
Graduate Ramanujan Summation, Variations of
  • · Replies 7 ·
Replies
7
Views
2K
MHB Interpolating Points with Continuous Modular Functions?
  • · Replies 5 ·
Replies
5
Views
2K
Graduate Memory issues in numerical integration of oscillatory function
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Finding the Largest (or smallest) Value of a Function - given some constant symmetric errors
  • · Replies 3 ·
Replies
3
Views
2K
Insights Series in Mathematics: From Zeno to Quantum Theory
  • · Replies 2 ·
Replies
2
Views
3K
MHB Is x^(2/3)(5/2-x) a Continuous Function for All Values of x?
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Continuity of Mean Value Theorem
  • · Replies 12 ·
Replies
12
Views
3K