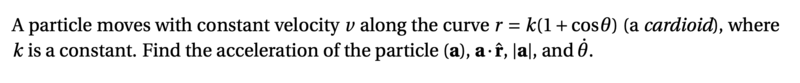guyvsdcsniper
- 264
- 37
- Homework Statement
- A particle moves with constant velocity v along the curve r = k(1+cosθ) (a cardioid), where
k is a constant. Find the acceleration of the particle (a), a· rˆ, |a|, and θ˙.
- Relevant Equations
- a = dV/dt
I am trying to follow the solution to the following problem, both linked in the attachment.
When trying to find the acceleration, a, that should be taking the derivative of r, the position formula twice. When doing so I get v = -ksinθ and a = -kcosθ. The attached work shows v being -(ksinθ)θ' which also leads to them getting a different answer for acceleration. Am i approaching this problem the wrong way?
When trying to find the acceleration, a, that should be taking the derivative of r, the position formula twice. When doing so I get v = -ksinθ and a = -kcosθ. The attached work shows v being -(ksinθ)θ' which also leads to them getting a different answer for acceleration. Am i approaching this problem the wrong way?