- #1
PainterGuy
- 940
- 69
Hi,
This thread is an extension of this discussion where @DrClaude helped me. I thought that it'd be better to separate this question.
I couldn't find any other way to post my work other than as images so if any of the embedded images are not clear, just click on them. It'd make them clearer. I'd really appreciate if you can help me.
Original expression:
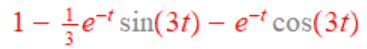
Laplace transform of the expression:
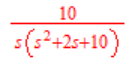
The graph of the expression is shown below.
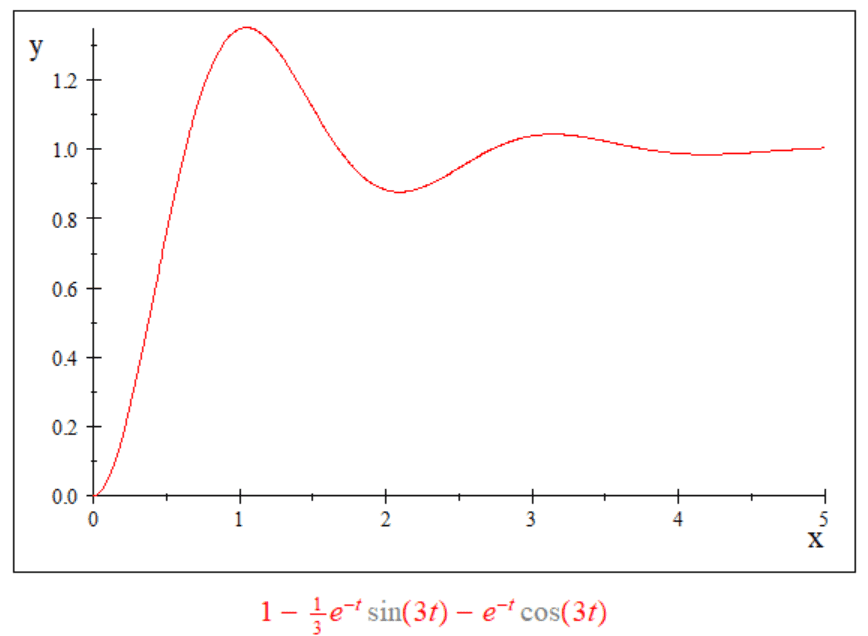



High res image for the above embedded image: https://imagizer.imageshack.com/img924/2191/JaiscO.jpg

High res image for the above embedded image: https://imagizer.imageshack.com/img921/3007/iPI3pi.jpg
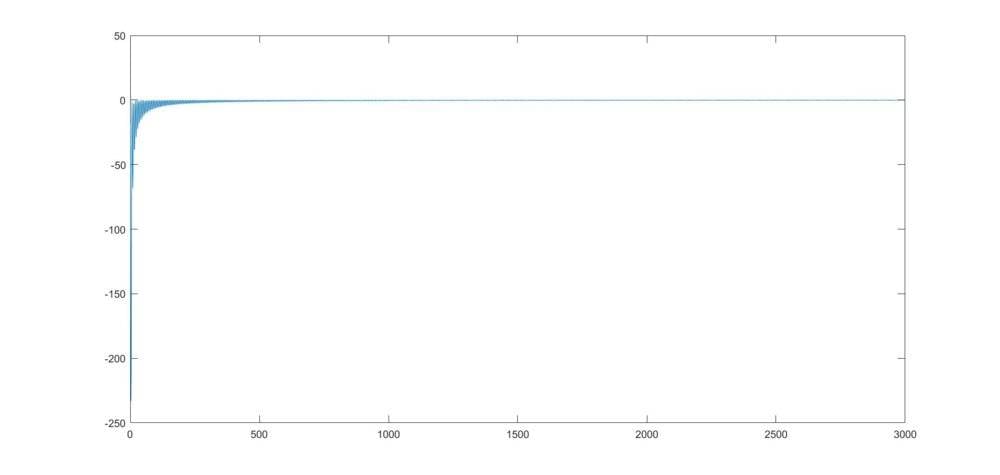
Sadly there is something wrong and I'm not getting the original f(t)=1-(1/3)e^(-t)sin(3t)-e^(-t)cos(3t). Please see the plot below. Where am I going wrong?
This thread is an extension of this discussion where @DrClaude helped me. I thought that it'd be better to separate this question.
I couldn't find any other way to post my work other than as images so if any of the embedded images are not clear, just click on them. It'd make them clearer. I'd really appreciate if you can help me.
Original expression:
Laplace transform of the expression:
The graph of the expression is shown below.
High res image for the above embedded image: https://imagizer.imageshack.com/img924/2191/JaiscO.jpg
High res image for the above embedded image: https://imagizer.imageshack.com/img921/3007/iPI3pi.jpg
Matlab:
clear all; close all; clc;
sig=1;
b=2;
t=linspace(0,30,3000);
for it=1:3000 %index for t varible
f=@(w)(1/pi).*(((10.*(sig.^3-sig.*w.^2+b.*sig.^2+10.*sig-2.*sig.*w.^2-b.*w.^2))/(sqrt(w.^6+w.^4.*(b.^2+2.*b.*sig+3.*sig.^2-20)+w.^2.*(2.*b.^2.*sig.^2+4.*b.*sig.*(sig.^2+5)+3.*sig.^4+100)+(b.^2.*sig.^2+2.*b.*sig.*(sig.^2+10)+sig.^4+20.*sig.^2+100).*sig^2))).*cos(w.*t(it))+(10.*(2.*sig.^2.*w+sig.*b.*w+w.*sig.^2-w.^3+b.*sig.*w+10.*w)/(sqrt(w.^6+w.^4.*(b.^2+2.*b.*sig+3.*sig.^2-20)+w.^2.*(2.*b.^2.*sig.^2+4.*b.*sig.*(sig.^2+5)+3.*sig.^4+100)+(b.^2*sig.^2+2.*b.*sig.*(sig.^2+10)+sig.^4+20.*sig.^2+100).*sig.^2))).*sin(w.*t(it)));
F(it)=integral(f,0,100); %evaluating the integral from w=0 to w=100
endplot(F) % F is inverse Fourier transform of f(t)Sadly there is something wrong and I'm not getting the original f(t)=1-(1/3)e^(-t)sin(3t)-e^(-t)cos(3t). Please see the plot below. Where am I going wrong?
Attachments
Last edited: