Albert1
- 1,221
- 0
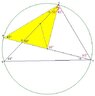
$\triangle ABC , \angle ABC=45^o,\,\, point \,\, D\,\, on \,\, \,\overline{BC} $
$and,\,\, 2\overline{BD}=\overline{CD},\,\, \angle DAB=15^o$
$find :\,\, \angle ACB=?$
$and,\,\, 2\overline{BD}=\overline{CD},\,\, \angle DAB=15^o$
$find :\,\, \angle ACB=?$