SUMMARY
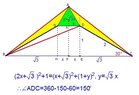
The problem involves triangle ABC, where sides AB and AC are equal, and point D lies inside the triangle such that AB = AC = BD. Given that angle DCB measures 30 degrees, the objective is to determine the measure of angle ADC. The solution requires applying properties of isosceles triangles and the relationships between angles formed by intersecting lines.
PREREQUISITES
- Understanding of isosceles triangles and their properties
- Knowledge of angle relationships in triangles
- Familiarity with geometric constructions and proofs
- Basic trigonometry concepts
NEXT STEPS
- Study the properties of isosceles triangles in depth
- Learn about angle chasing techniques in geometry
- Explore geometric proofs involving inner points of triangles
- Investigate the use of geometric software for visualizing triangle properties
USEFUL FOR
Students studying geometry, mathematics educators, and anyone interested in solving geometric problems involving triangles and angle relationships.