evinda
Gold Member
MHB
- 3,741
- 0
Hello! (Wave)
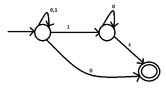
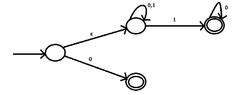
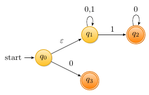
I want to construct a dfa that recognizes the language $((0 \cup 1)^{\ast} 1 0^{\ast}) \cup 0$.
I have thought of the following NFA:
View attachment 5833
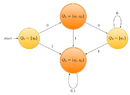
But I am facing difficulties on converting this to a NFA. Could you give me a hint how we could do this?
I want to construct a dfa that recognizes the language $((0 \cup 1)^{\ast} 1 0^{\ast}) \cup 0$.
I have thought of the following NFA:
View attachment 5833
But I am facing difficulties on converting this to a NFA. Could you give me a hint how we could do this?