evinda
Gold Member
MHB
- 3,741
- 0
I like Serena said:I don't think so.
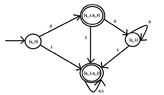
We can convert it to states with sets of the original states.
For $\epsilon$-transitions, we just need to draw in additional states that might be reached with an $\epsilon$-transition. (Thinking)
I haven't really understood what we have to do... (Worried)
By ignoring the $\epsilon$-transition, we have the following. Right?
$\begin{matrix}
& 0 & 1\\
\{q_0\} & \{q_3\} &\varnothing \\
\{q_3\} & \varnothing & \varnothing
\end{matrix}$
By including the $\epsilon$-transition, we have the following additional transitions:
$q_0 \overset{0,1}{\to} q_1$ and $q_0 \overset{1}{\to} q_3$
So do we have the following transition function?
$\begin{matrix}
& 0 & 1\\
\{q_0\} & \{q_1,q_3\} &\{q_1, q_3\} \\
\{q_3\} & \varnothing & \varnothing
\end{matrix}$Or have I understood it wrong? (Sweating)