Finding distance between Earth and Moon in gravitational fields

[Bolter]

Homework Statement

Calculate the distance between 2 masses in a gravitational field

Calculate the height reached when a person jumps on a planet

Relevant Equations

Orbital period
gravitational field strength

Here are 2 questions that I have tried to answer and was hoping if these are right ways to go about it?

Q1) Find the distance in meters (m) between centre of the Moon and the centre of the Earth, assuming that the Moon moves in a circular orbit with a period of 27.5 days. Take the mass of the Earth as 6.0 × 10^24 kg. Assume that the distance between the Earth and the Moon is much larger than the radii of both planets

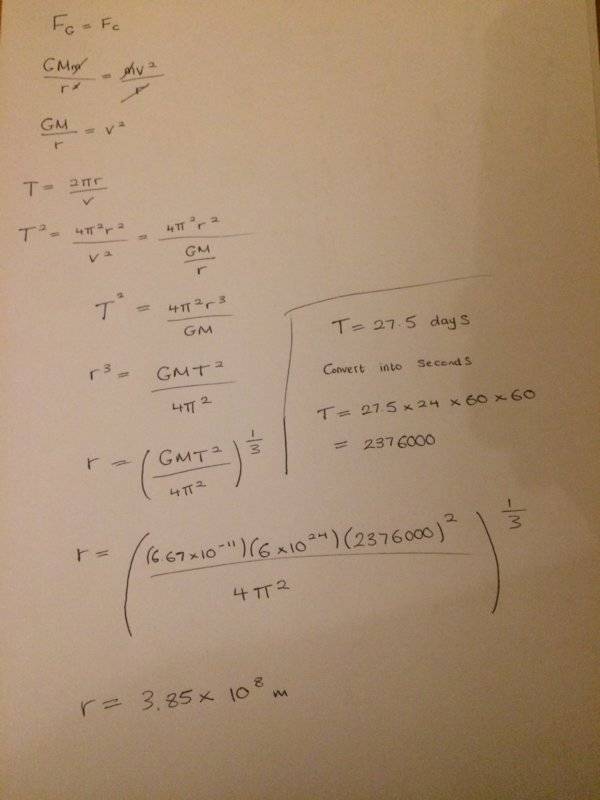
Q2) If a person can jump a vertical height of 1.3 m on the Earth, how high could he jump (applying the same effort as on the Earth) on a planet with the same density as the Earth, but only half the radius.

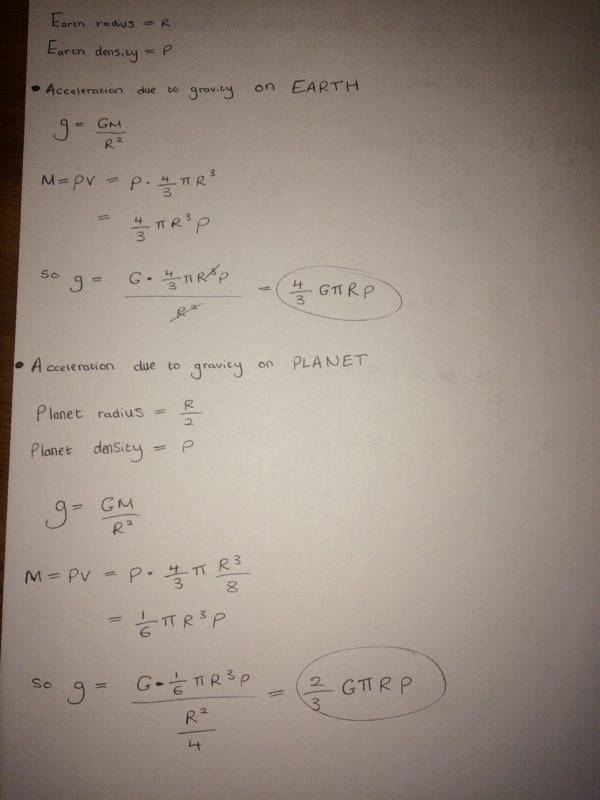
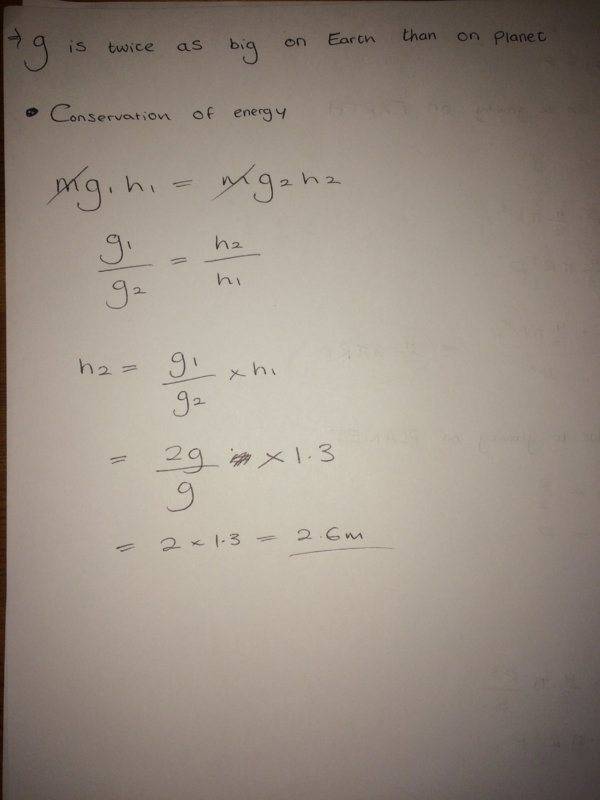
Any help would be appreciated! Thanks

 

[gneill]

Your work looks good to me.

 

[Bolter]

Your work looks good to me.

Ok thank you so much

 

[TSny]

Looks good to me, too. Note that once you have the expression $g = \frac{4}{3}G \pi \rho R$ you can see that $g$ is just proportional to $R$ for fixed $\rho$. So, you can see $g_2$ will be half of $g_1$.

 

[Bolter]

Looks good to me, too. Note that once you have the expression $g = \frac{4}{3}G \pi \rho R$ you can see that $g$ is just proportional to $R$ for fixed $\rho$. So, you can see $g_2$ will be half of $g_1$.

Ah yes I can see this relationship, much easier to use the proportionality relationship then to identify how much bigger or smaller g1 will be to g

 

[kuruman]

Ah yes I can see this relationship, much easier to use the proportionality relationship then to identify how much bigger or smaller g1 will be to g

You are learning to think like a physicist.