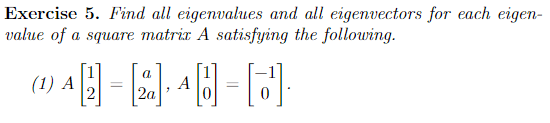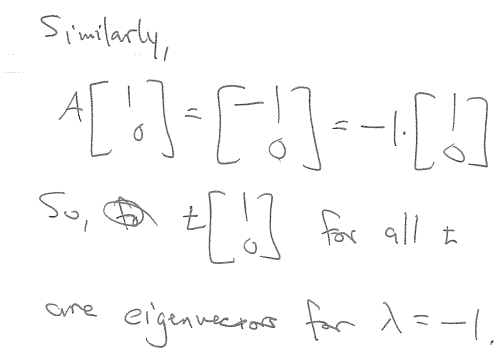Homework Help Overview
The discussion revolves around finding eigenvalues and eigenvectors related to sub-matrices, focusing on the properties of eigenvectors when scaled by a real number.
Discussion Character
- Conceptual clarification, Mathematical reasoning
Approaches and Questions Raised
- Participants explore the implications of scaling eigenvectors by a scalar and question how this relates to the definitions of eigenvalues and eigenvectors.
Discussion Status
Several participants have provided insights into the relationship between eigenvectors and their scalar multiples, with some clarifying definitions and others rephrasing statements to align with formal definitions. There appears to be a productive exchange of ideas without explicit consensus on a single interpretation.
Contextual Notes
Participants are considering specific conditions under which the properties of eigenvalues and eigenvectors hold, particularly in relation to the parameter 'a' in the context of the problem.