Finding Hydrogen eigenfunction u(2,0)

[unscientific]

Taken from Physics of Quantum Mechanics, by James Binney.

I try to calculate $u_{n}^{l=n-2}$, something goes wrong:

Starting, we define operator A by:

$$A_{n-2} = \frac{a_0}{\sqrt 2}\left(\frac{i}{\hbar}p_r + \frac{1-n}{r} + \frac{Z}{(n-1)a_0}\right)$$

Substituting $p_r = -i\hbar (\frac{\partial}{\partial r} + \frac{1}{r})$:

$$A_{n-2} = \frac{a_0}{\sqrt 2}\left( \frac{\partial}{\partial r} + \frac{2-n}{r} + \frac{Z}{(n-1)a_0}\right)$$

Thus, we want to solve:

$$\left(\frac{\partial}{\partial r} + \frac{2-n}{r} + \frac{Z}{(n-1)a_0} \right) u_{n}^{l=n-2} = 0$$

Solving by integrating factor method, we obtain:

$$u_n^{l=n-2} = A r^{n-2} e^{\frac{Z}{(n-1)a_0}r}$$

Normalizing,

$$u_n^{l=n-2} = \frac{1}{\sqrt{[2(n-1)]!}} \left(\frac{2Z}{(n-1)a_0}\right)^{\frac{3}{2}} \left(\frac{2Z}{(n-1)a_0}\right)^{n-2} e^{-\frac{Z}{(n-1)a_0}r}$$

This is similar to $u_n^{l=n-1}$, simply replace n by n-1:

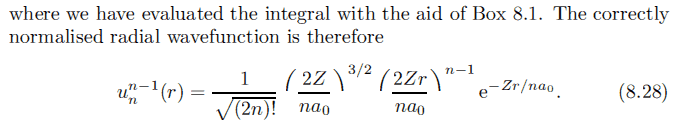
But when I substitute n = 2, so l = 0, I get $u_2^0 = \frac{1}{\sqrt 2} \left(\frac{2Z}{a_0}\right)^{\frac{3}{2}} e^{-\frac{Z}{a_0}r}$

I get a completely different result from the book:

I'm not sure what's wrong with my derivation?

 

[Bill_K]

The copy of Binney I'm looking at is slightly different from yours, so bear with me, but the equation you're trying to use,

A_n-1|n, n-1> = 0

is only for (as he says) "the radial wavefunction of the circular orbit with angular momentum ℓ = n - 1." That is, it gives the wavefunctions along the diagonal in Table 8.1. To get the other wavefunctions you need to start with one of these wavefunctions and one or more times apply A†. This will step you up in the table, along one of the columns.

"Applications of A† should generate the wavefunctions for ℓ < n - 1."

 

[unscientific]

The copy of Binney I'm looking at is slightly different from yours, so bear with me, but the equation you're trying to use,

A_n-1|n, n-1> = 0

is only for (as he says) "the radial wavefunction of the circular orbit with angular momentum ℓ = n - 1." That is, it gives the wavefunctions along the diagonal in Table 8.1. To get the other wavefunctions you need to start with one of these wavefunctions and one or more times apply A†. This will step you up in the table, along one of the columns.

"Applications of A† should generate the wavefunctions for ℓ < n - 1."

Ah, so by applying A† to $u_n^{l=n-1}$ it will give $u_n^{l=n-2}$?

 

[Bill_K]

Ah, so by applying A† to $u_n^{l=n-1}$ it will give $u_n^{l=n-2}$?

That's my understanding. Try it and see!

 

[unscientific]

That's my understanding. Try it and see!

It's mentioned right below the screenshot, I can't believe I missed it..

I tried it, and normalized and it came out right!